Ayuda con una Integral
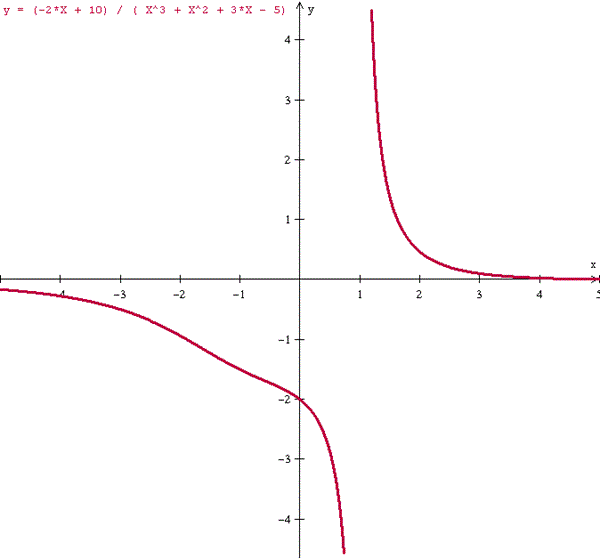
En el último examen de matemáticas de mi carrera (Bioquímica) apareció este ejercicio. Lo estoy intentando resolver pero no encuentro la manera de integrar la función. El enunciado es: Calcular el área del recinto encerrado entre la gráfica de la función y el eje OX.
f(x)= (-2X + 10) / ( X*3 + X*2 + 3X - 5)
Me dice también que "X" es mayor o igual a 2
Supongo que los límites de integración son 2 y 5, ya que es donde corta la función al eje X.
La integral soy incapaz de resolverla.
f(x)= (-2X + 10) / ( X*3 + X*2 + 3X - 5)
Me dice también que "X" es mayor o igual a 2
Supongo que los límites de integración son 2 y 5, ya que es donde corta la función al eje X.
La integral soy incapaz de resolverla.
Respuesta de diodo1234
1
Ando un poco pillado de tiempo y soy bastante lento resolviendo integrales, por ahora te doy las pautas, debes encontrar las raíces o soluciones del polinomio divisor ( X*3 + X*2 + 3X - 5), a simple vista veo que una de ellas es 1. Cuando las tengas el polinomio te quedará igual a (x-a)*(x-b)*(x-1) donde a, b son las soluciones que te faltan.
Luego descompones en tres cocientes, e integras cada uno de ellos.
Puedes ver como en http://html.rincondelvago.com/metodos-de-integracion.html
Apartado "Método de integración por descomposición en fracciones simples"
Si ves que no te sale y no te corre prisa te lo miro.
Luego descompones en tres cocientes, e integras cada uno de ellos.
Puedes ver como en http://html.rincondelvago.com/metodos-de-integracion.html
Apartado "Método de integración por descomposición en fracciones simples"
Si ves que no te sale y no te corre prisa te lo miro.
1 respuesta más de otro experto
Respuesta de Valero Angel Serrano Mercadal
1
Ya se que aquí se emplean simplificaciones que conducen a engaño. Confírmame si quieres decir esto.
(-2X + 10) / ( X^3 + X^2 + 3X - 5)
Es una integral racional de la que ni siquiera nos dan las raíces del denominador, por suerte se ve que x=1 es una solución fácil.
Ahora tengo poco tiempo. Si no puedo resolverla de inmediato espera otras ocho horas.
(-2X + 10) / ( X^3 + X^2 + 3X - 5)
Es una integral racional de la que ni siquiera nos dan las raíces del denominador, por suerte se ve que x=1 es una solución fácil.
Ahora tengo poco tiempo. Si no puedo resolverla de inmediato espera otras ocho horas.
Si si, esa es la función.
Sigo intentándola y nada. Es desesperante jajajajaja.
Sigo intentándola y nada. Es desesperante jajajajaja.
Vamos con la resolución.
Por Rufini o haciendo la división larga que llaman, tendrás que tras dividir por (x-1) el denominador queda factorizado así:
X^3 + X^2 + 3X - 5 =(X-1)(X^2 + 2X + 5)
El segundo factor no tiene respuestas reales.
Hay una serie de métodos para descomponer las fracciones de polinomios en suma de otras fracciones más simples
En el caso que nos toca (y siguiendo la teoría de los libros) estas fracciones serán de la forma:
a/(x-1) + (bx+c)/(x^2+2x +5)
Si hacemos la suma de esas dos fracciones, poniendo como denominador el producto de los denominadores, tendremos que multiplicar cada numerador por el denominador contrario y nos daría este numerador:
ax^2 + 2ax + 5a + bx^2 - bx + cx - c
Este numerador tiene que ser idéntico al que teníamos original porque el denominador también es el mismo, luego:
ax^2 + 2ax + 5a + bx^2 - bx + cx - c = -2x + 10
(a+b)x^2 + (2a-b+c)x + (5a - c) = 2x +10
Esta igualdad es la de un polinomio, luego deben ser iguales todos los coeficientes, en x^2, en x y el independiente. De ello se decuden las tres ecuaciones que encabezan las tres líneas siguientes y que de paso voy resolviendo.
a + b = 0 ==>
2a - b + c = -2 ==> 3a + c = -2
5a - c = 10 ==> 5a = 8 ==> a = 5/8 ==> b = -5/8 ==> c= 25/8 - 10 = -55/8
Descanso un poco para asegurarme que esos son los coeficientes verdaderos. El problema no es nada fácil. Y aún queda lo de los límites de integración, porque fíjate como es la gráfica:
Tiene una asíntota en x=1. Según que límites tomemos puede salir hasta una integral impropia que no sé si sería convergente.
Bueno, mientras piensas que límirtes tomamos continuaré con la integral impropia.
Por Rufini o haciendo la división larga que llaman, tendrás que tras dividir por (x-1) el denominador queda factorizado así:
X^3 + X^2 + 3X - 5 =(X-1)(X^2 + 2X + 5)
El segundo factor no tiene respuestas reales.
Hay una serie de métodos para descomponer las fracciones de polinomios en suma de otras fracciones más simples
En el caso que nos toca (y siguiendo la teoría de los libros) estas fracciones serán de la forma:
a/(x-1) + (bx+c)/(x^2+2x +5)
Si hacemos la suma de esas dos fracciones, poniendo como denominador el producto de los denominadores, tendremos que multiplicar cada numerador por el denominador contrario y nos daría este numerador:
ax^2 + 2ax + 5a + bx^2 - bx + cx - c
Este numerador tiene que ser idéntico al que teníamos original porque el denominador también es el mismo, luego:
ax^2 + 2ax + 5a + bx^2 - bx + cx - c = -2x + 10
(a+b)x^2 + (2a-b+c)x + (5a - c) = 2x +10
Esta igualdad es la de un polinomio, luego deben ser iguales todos los coeficientes, en x^2, en x y el independiente. De ello se decuden las tres ecuaciones que encabezan las tres líneas siguientes y que de paso voy resolviendo.
a + b = 0 ==>
2a - b + c = -2 ==> 3a + c = -2
5a - c = 10 ==> 5a = 8 ==> a = 5/8 ==> b = -5/8 ==> c= 25/8 - 10 = -55/8
Descanso un poco para asegurarme que esos son los coeficientes verdaderos. El problema no es nada fácil. Y aún queda lo de los límites de integración, porque fíjate como es la gráfica:
Tiene una asíntota en x=1. Según que límites tomemos puede salir hasta una integral impropia que no sé si sería convergente.
Bueno, mientras piensas que límirtes tomamos continuaré con la integral impropia.
Tanto correr para perder ahora todo el tiempo por estar mal.
Es a=8/5 y no 5/8 como había puesto. Luego:
a = 8/5
b =-8/5
c= 5(8/5) -10 = -2
Usaré el dolar copmo signo de integración, es lo mejor que se puede hacer con este editor tan simple. Las fracciones simples halladas hacen que la integral sea esta
(8/5)$(x-1)dx + $[-(8/5)x - 2] / (x^2 + 2x + 5) dx =
(8/5)ln|x-1| - (2/5) $[(4x +5) / (x^2 + 2x + 5)] dx
Bueno, como te decía tengo que dejarlo por el momento. La integral es complicada, te puedo adelantar el resultado que me proporciona Máxima, pero si quieres ver como se resuelve no podré hacerlo hasta varias horas.
Es (8/5)ln|x-1| -(2/5) [2ln|x^2+2x-5| + arctg((2x+2)/4)/2]
Para mí que este problema es muy complicado, aunque yo ya llevaba muchísimos años sin practicar y no me acuerdo como se resolvía esta última integral.
Es a=8/5 y no 5/8 como había puesto. Luego:
a = 8/5
b =-8/5
c= 5(8/5) -10 = -2
Usaré el dolar copmo signo de integración, es lo mejor que se puede hacer con este editor tan simple. Las fracciones simples halladas hacen que la integral sea esta
(8/5)$(x-1)dx + $[-(8/5)x - 2] / (x^2 + 2x + 5) dx =
(8/5)ln|x-1| - (2/5) $[(4x +5) / (x^2 + 2x + 5)] dx
Bueno, como te decía tengo que dejarlo por el momento. La integral es complicada, te puedo adelantar el resultado que me proporciona Máxima, pero si quieres ver como se resuelve no podré hacerlo hasta varias horas.
Es (8/5)ln|x-1| -(2/5) [2ln|x^2+2x-5| + arctg((2x+2)/4)/2]
Para mí que este problema es muy complicado, aunque yo ya llevaba muchísimos años sin practicar y no me acuerdo como se resolvía esta última integral.
¡Vaya día llevo! Oldivate de casi todo lo que hice.
Volvamos atrás. La descomposición en fracciones simples era de la forma:
a/(x-1) + (bx+c)/(x^2+2x+5)
Las ecuaciones que habíamos calculado eran:
a + b = 0 ==>
2a - b + c = -2 ==> 3a + c = -2
5a - c = 10 ==> 8a = 8 ==> a = 1 ==> b= -1 ==> c = -5
Luego la integral una vez descompuesta es:
$(1/x-1)dx + $ (-x - 5)/(x^2+2x+5)dx =
ln|x-1| - $(x+5)/(x^2+2x+5)dx
En vez de usar fórmulas que se olvidan, lo haremos deduciendo.
No nos sirve separar la integral en los dos sumandos que tiene. La idea de este tipo de integral es descomponerla de modo que sea exactamente la derivada de un logaritmo neperiano más la derivada de un arco tangente. Por lo tanto, el primer sumando tendrá que tener como numerador la derivada del denominador convenientemente multiplicada por una constante para que se apropie de todo el monomio en por, y el segundo sumando tendrá por numerador una constante, nada de x.
La derivada del denominador es 2x+2
La constante será aquella que al multiplicar por la derivada nos de el coeficiente en x del numerador. Como el numerador tiene 1 de coeficiente en x, será 1/2
la constante por la derivada nos da (1/2)(2x+2) = x+1
Pues ese x+1 irá a la primera fracción y lo que queda x+5 - (x+1) = 4 irá al numerador de la segunda fracción
$[(x + 5) / (x^2+2x+5)] = $[(x+1) / (x^2+2x+5)] dx + $4 / [(x^2+2x+5)]dx =
(1/2) ln |x^2 + 2x + 5| + 4$1/[(x^2+2x+5)]dx =
Para la integral que sigue quedando hay que usar otro truco que es poner el denominador como suma de dos cuadrados uno que sea de la forma (x+a)^2 y el otro será la raíz cuadrada de lo que quede. Esto es muy sencillo, si el denominador es de la forma
x^2 + bx + c
se toma como primer cuadrado
(X + b/2)^2 que nos da x^2 + bx + (b^2)/4 y el otro cuadrado será lo que falta para tener x^2 + bx + c que es c-(b^2)/4
En nuestro caso b=2 ==> b/2 = 1 ==> (b^2)/4 = 1 ==> c-(b^2)/4 = 5-1 = 4
$1 / [(x^2+2x+5)]dx =$1 / [(x+1)^2 + 4]dx =
Tenemos que conseguir que el segundo sumando del denominador sea 1. Para ello multiplicamos y dividimos el denominador por 4
= (1/4) $1 / ([(x+1)/2]^2 +1)dx =
Solo falta 1/2 dentro del integrando para tener la derivada de arctg((x+1)/2)
= (1/4)2$(1/2)/([(x+1)/2]^2 +1)dx = (1/2) arctg ((x+1)/2)
Vamos a recolectar
$(-2x+10)/(X^3 + X^2 + 3X - 5) dx =ln|x-1| - $(x+5)/(x^2+2x+5)dx
= ln|x-1| - (1/2) ln |x^2 + 2x + 5| - 4$1/[(x^2+2x+5)]dx =
= ln|x-1| - (1/2) ln |x^2 + 2x + 5| -4 (1/2) arctg((x+1)/2) =
= ln|x-1| - (1/2) ln |x^2 + 2x + 5| - 2·arctg((x+1)/2) + C
Esa es la integral indefinida, se puede comprobar fácilmente que lo es.
Pues ahora si que te pido ya que fijes los límites de integración si quieres que continué o si ya no me necesitas más que puntúes y cierres la pregunta.
Un saludo.
ln|x-1| - $(x+5)/(x^2+2x+5)dx
ln|x-1| - (2/5) $[(4x +5) / (x^2 + 2x + 5)] dx =
(8/5)ln|x-1| - (2/5) {2ln|x^2 + 2x + 5| + $1 / [(x^2+2x+5)]dx}=
(8/5)ln|x-1| - (4/5)ln|x^2 + 2x + 5| - (2/5)$1 / [(x^2+2x+5)]dx =
(8/5)ln|x-1| - (4/5)ln|x^2 + 2x + 5| - (2/5)(1/2) arctg ((x+1)/2) =
(8/5)ln|x-1| - (4/5)ln|x^2 + 2x + 5| - (1/5)arctg[(x+1)/2] + C
Volvamos atrás. La descomposición en fracciones simples era de la forma:
a/(x-1) + (bx+c)/(x^2+2x+5)
Las ecuaciones que habíamos calculado eran:
a + b = 0 ==>
2a - b + c = -2 ==> 3a + c = -2
5a - c = 10 ==> 8a = 8 ==> a = 1 ==> b= -1 ==> c = -5
Luego la integral una vez descompuesta es:
$(1/x-1)dx + $ (-x - 5)/(x^2+2x+5)dx =
ln|x-1| - $(x+5)/(x^2+2x+5)dx
En vez de usar fórmulas que se olvidan, lo haremos deduciendo.
No nos sirve separar la integral en los dos sumandos que tiene. La idea de este tipo de integral es descomponerla de modo que sea exactamente la derivada de un logaritmo neperiano más la derivada de un arco tangente. Por lo tanto, el primer sumando tendrá que tener como numerador la derivada del denominador convenientemente multiplicada por una constante para que se apropie de todo el monomio en por, y el segundo sumando tendrá por numerador una constante, nada de x.
La derivada del denominador es 2x+2
La constante será aquella que al multiplicar por la derivada nos de el coeficiente en x del numerador. Como el numerador tiene 1 de coeficiente en x, será 1/2
la constante por la derivada nos da (1/2)(2x+2) = x+1
Pues ese x+1 irá a la primera fracción y lo que queda x+5 - (x+1) = 4 irá al numerador de la segunda fracción
$[(x + 5) / (x^2+2x+5)] = $[(x+1) / (x^2+2x+5)] dx + $4 / [(x^2+2x+5)]dx =
(1/2) ln |x^2 + 2x + 5| + 4$1/[(x^2+2x+5)]dx =
Para la integral que sigue quedando hay que usar otro truco que es poner el denominador como suma de dos cuadrados uno que sea de la forma (x+a)^2 y el otro será la raíz cuadrada de lo que quede. Esto es muy sencillo, si el denominador es de la forma
x^2 + bx + c
se toma como primer cuadrado
(X + b/2)^2 que nos da x^2 + bx + (b^2)/4 y el otro cuadrado será lo que falta para tener x^2 + bx + c que es c-(b^2)/4
En nuestro caso b=2 ==> b/2 = 1 ==> (b^2)/4 = 1 ==> c-(b^2)/4 = 5-1 = 4
$1 / [(x^2+2x+5)]dx =$1 / [(x+1)^2 + 4]dx =
Tenemos que conseguir que el segundo sumando del denominador sea 1. Para ello multiplicamos y dividimos el denominador por 4
= (1/4) $1 / ([(x+1)/2]^2 +1)dx =
Solo falta 1/2 dentro del integrando para tener la derivada de arctg((x+1)/2)
= (1/4)2$(1/2)/([(x+1)/2]^2 +1)dx = (1/2) arctg ((x+1)/2)
Vamos a recolectar
$(-2x+10)/(X^3 + X^2 + 3X - 5) dx =ln|x-1| - $(x+5)/(x^2+2x+5)dx
= ln|x-1| - (1/2) ln |x^2 + 2x + 5| - 4$1/[(x^2+2x+5)]dx =
= ln|x-1| - (1/2) ln |x^2 + 2x + 5| -4 (1/2) arctg((x+1)/2) =
= ln|x-1| - (1/2) ln |x^2 + 2x + 5| - 2·arctg((x+1)/2) + C
Esa es la integral indefinida, se puede comprobar fácilmente que lo es.
Pues ahora si que te pido ya que fijes los límites de integración si quieres que continué o si ya no me necesitas más que puntúes y cierres la pregunta.
Un saludo.
ln|x-1| - $(x+5)/(x^2+2x+5)dx
ln|x-1| - (2/5) $[(4x +5) / (x^2 + 2x + 5)] dx =
(8/5)ln|x-1| - (2/5) {2ln|x^2 + 2x + 5| + $1 / [(x^2+2x+5)]dx}=
(8/5)ln|x-1| - (4/5)ln|x^2 + 2x + 5| - (2/5)$1 / [(x^2+2x+5)]dx =
(8/5)ln|x-1| - (4/5)ln|x^2 + 2x + 5| - (2/5)(1/2) arctg ((x+1)/2) =
(8/5)ln|x-1| - (4/5)ln|x^2 + 2x + 5| - (1/5)arctg[(x+1)/2] + C