Ayuda con problema de función cuadrática, urge para prueba
Estoy realizando mi práctica de examen y me encontré con este ejercicio, espero una buena ayudita.
La entrada de un edificio tiene la forma de un arco parabólico y mide 9 pies de alto en el centro y 6pie de ancho en la base. Si hay que meter una caja rectangular de 8pie de alto, ¿Cuál es el ancho máximo que puede tener la caja?
1 Respuesta
Aquí tienes el dibujo, pero hay que resolverlo analíticamente.
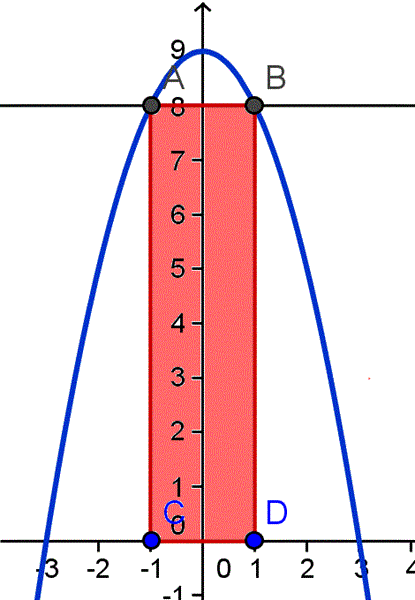
Pondremos la parábola centrada para mayor facilidad. Por tener un ancho de 6 pies pasara por los puntos (-3,0) y (3,0) Y por tener un alto de 9 pies pasara por el punto (0,9)
La parábola tendrá por ecuación
y = ax^2 + by + c
Para que pase por esos tres puntos debe cumplirse
0 = a(-3)^2 -3b + c
0 = a(3)^2 + 3b + c
9 = a(0)^2 +0b + c
Ya operadas son
9a - 3b + c = 0
9a + 3b + c = 0
c = 9
Poniendo el valor c=9 las dos primeras quedad
9a - 3b + 9 = 0
9a + 3b + 9 = 0
Sumándolas queda
18a + 18 = 0
18a = -18
a = -1
Y finalmente vamos con este valor a la primera
-9 -3b + 9 = 0
-3b=0
b = 0
Luego ya tenemos los tres valores y la ecuación de la parábola es:
y = -x^2+9
Tal vez si tuvieras bastante practica habrías dado con ella sin resolver estas ecuaciones, pero es el método general que sirve para ejercicios más complicados
Y una tenemos la ecuación de la parábola tenemos que ver cuál es el ancho que tiene a 8 pies de altura. Sustituimos la y de la ecuación por esa altura
8 = -x^2+9
x^2 = 9-8 = 1
x=+1 y -1
Luego los puntos A y B de la figura son
(-1,8) y (1,8)
La anchura es la distancia entre ellos, solo tiene componente horizontal luego nos podemos dejar de calcular raíces cuadradas de sumas de cuadrados, simplemente es restar una componente de x a la otra 1-(-1) = 2
Luego la anchura máxima que puede tener la caja es 2 pies.
Y eso es todo.
