Cálculo de la distancia del Sol a Mercurio
¿Cuál es la distancia del Sol a Mercurio, cuando este planeta se encuentra en el ángulo de máxima
elongación y la Tierra está en el punto más cercano al Sol?
Para responder, toma en cuenta las siguientes consideraciones:
a) Con los datos de la Tabla de cuerpos celestes, realiza la gráfica de las órbitas de Mercurio y la Tierra, considera al Sol como uno de los focos y sitúalo en el origen del sistema de coordenadas.
b) Para ambas órbitas, ubica el perihelio sobre el eje de las abscisas en el sentido negativo y el afelio en el
sentido positivo.
c) Determina la posición de la Tierra.
d) Encuentra cuál es la posición de mercurio, cuando se encuentra en el ángulo de máxima elongación.
e) Determina cuál es la distancia del Sol a Mercurio, medida en U.A.
Para resolver este problema considera que la distancia Sol-Tierra es 150 millones de Km.
1 respuesta
Hace algún año respondí esta pregunta, me costó mucho y tuvieron que explicarme que era eso de la elongación, que ya lo he olvidado y tampoco me supieron dar todo lo que necesitaba y tuve que hacer algunas suposiciones al final. Lamentablemente han retirado la respuesta de la base de TodoExpertos y tendría que empezar de nuevo sin recordar lo que hice.
Entonces necesito más explicaciones sobre la elongación y otras cosas que puedan surgir. Recuerdo que me mandaron un gráfico donde salían la tierra el sol y mercurio, no se si tú lo tendrás.
En todo caso no me puedo poner ahora mismo con esta pregunta porque me llevaría todo el tiempo y tengo muchas pendientes de responder. Ayúdame dándome esos datos que te digo.
Si es un problema poco confuso, por esa razón pido de tu apoyo, espero puedas ayudarme,mira los datos que tengo son estos:
Se denomina elongación de un planeta al ángulo que forma el planeta, la Tierra
y el Sol, medido en el plano que contiene a estos tres cuerpos celestes y teniendo siempre a la Tierra como vértice del ángulo.
Los planetas de nuestro Sistema Solar se dividen en:
• Planetas inferiores, si su órbita es interna con respecto a la de la Tierra.
• Planetas superiores, cuando la órbita es externa con respecto a la de la Tierra.
Cuando los planetas son inferiores su elongación tiene un valor máximo, que se alcanza
cuando la línea Tierra-Planeta es tangente a la órbita de ese planeta.
Gracias.
No tengo la solución pero si se está mucho tiempo sin actividad retiran la pregunta. Manda ahora un comentario cualquiera para que siga activa.
Gracias.
Es que esta pregunta debe ser de Astronomía ¿no? Es la asignatura que no di en Matemáticas, preferí dar Álgebra III en su lugar.
Para que la pregunta se pueda responder creo que se deben dar estas circunstancias. Que la Tierra y Mercurio tengan la órbita en el mismo plano y que además las elipses tengan el mimo eje longitudinal.
Solo así se puede empezar a calcular a través de los radios orbitales medios y las excentricidades las ecuaciones de movimiento de los dos planetas y calcular la tangente desde perihelio de la Tierra a la órbita de Mercurio.
¿Estas de acuerdo con lo que he dicho?
De la Wikipedia obtengo que la distancia mas corta es 147,1 millones de km y la mayor 152.1 millones de km
Eso significa que el eje mayor es 299.2 y el semieje mayor a=149.6
La distancia entre focos es 5 millones de km y la distancia foco-centro es 2.5 millones de km.
Por el teorema de Pitágoras esa distancia foco centro al cuadrado más el semieje menor a cuadrado es el cuadrado del semieje mayor
b^2 + 2.5^2 = 149.6^2
b^2 = 22380.16 - 6.25 =22373.91
b = 149.5791095
Tan apenas hay diferencia entre los semiejes, para no llevar tantos decimales pero que sean distintos tomaré b= 149.58
La ecuación de la elipse debe tener en cuenta que nos han hecho poner el origen en un foco en vez del centro (para fastidiar)
El centro de la elipse es (2.5, 0)
Luego la ecuación de la Tierra será:
$$\frac{(x-2.5)^2}{149.6^2}+\frac{y^2}{149.58^2}=1$$Mientras que Mercurio tiene un perihelio 45.943.700 Km y un afelio de 69.874.671 Km. Vamos a redondear y poner en millones de km al igual que la tierra, 45.94 y 69.87 millónes de km
Con lo cual el eje mayor es 115.81 y el semieje mayor es a57.905
La distancia entre focos es 115.81 - 2·57.905 = 23.93 luego la distancia foco centro es 11.965
Y el semieje menor es
b =sqrt(57.905^2-11.965^2) = 56.655
el centro de la elipse es (11.965, 0) luego la ecuación canónica es
$$\frac{(x-11.965)^2}{57.905^2}+\frac{y^2}{56.655^2}=1$$Este es la gráfica.
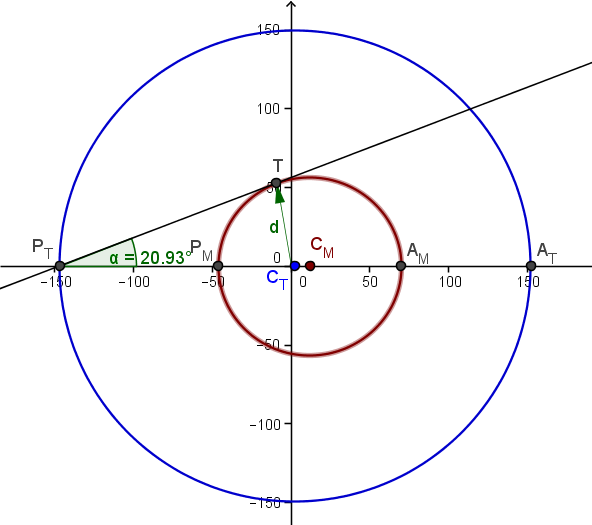
El perihelio de la tierra es (-149.6, 0)
Una recta que pase por el será
r : (-149.6, 0)+t(1,p)
debemos hacer que corte a la órbita de Mercurio en un solo punto
$$\begin{align}&\frac{(x-11.965)^2}{57.905^2}+\frac{y^2}{56.655^2}=1\\ &\\ &\frac{(-149.6+t -11.965)^2}{57.905^2}+\frac{t^2p^2}{56.655^2}=1\\ &\\ &56.655^2(t-161.565)^2+57.905^2t^2p^2 = 56.655^2·57.905^2\\ &\\ &t^2(56.655^2+57.905^2p^2)-t(323.13·56.655^2)+56.655^2(161.565^2-57.905^2)=0\\ &\\ &\text{Debe ser 0 el discriminante}\\ &(323.13·56.655^2)^2-4(56.655^2+57.905^2p^2)56.655^2(161.565^2-57.905^2)=0\\ &\\ &323.13^2·56.655^2-4(56.655^2+57.905^2p^2)(161.565^2-57.905^2)=0\\ &\\ &335143691.5 - (12839.1561+ 13411.9561p^2)22750.2602=0\\ &\\ &335143691.5-292094142 = 305125491.1p^2\\ &\\ &p=\sqrt{\frac{43049549.5}{305125491.1}}=0.3756168444\end{align}$$Madre mía, para morirse. Para orientarnos si lo hemos hecho bien, Geogebra ha calculado por el dibujo que el ángulo es 20.93º veamos si su tangente coincide con la pendiente de esta recta
tg(20.93º) =0.382462
Bueno, más o menos, Geogebra falla bastante en los cálculos.
Y conocida p se puede calcular t resolviendo la ecuación de segundo grado que queda sin discriminante
$$\begin{align}&t^2(56.655^2+57.905^2p^2)-t(323.13·56.655^2)+56.655^2(161.565^2-57.905^2)=0\\ &\\ &t =\frac{323.13·56.655^2}{2(56.655^2+57.905^2p^2)}=\\ &\\ &\\ &\frac{323.13·56.655^2}{2(56.655^2+57.905^2 \frac{43049549.5}{305125491.1})}=\\ &\\ &\\ &\frac{1037179.128}{7365.711174}=140.8118108\end{align}$$Con esto el punto de intersección será
x=-149.6 + 140.8118108 = -8.7881892
y = tp = 140.8118108 · 0.3756168444 = 52.89128797
Si, parece que afirma lo que dice el dibujo.
Luego la dichosa distancia de Mercurio al sol es
$$\begin{align}&\sqrt{(-8.7881892)^2+52.89128797^2}=\\ &\\ &53.61642111 \text{millones de km}\\ &53\,616\,421 km\end{align}$$No estaría bien que después de tantos cálculos con tantísimos decimales lo estropeáramos todo en la conversión de la UA. La UA es 149597871 km
d = 53616421 / 149597871 = 0.3584036366 UA
Aunque redondeé decimales al principio, la respuesta no es exacta del todo.
Y eso es todo, espero que te sirva y lo hayas entendido. Si no es así pregúntame. Y si ya está bien no olvides puntuar. Si encuentro la pregunta del tablón te la mando también para que la puntúes porque esta pregunta vale por varias de las normales.
