Análisis de cadenas de markov
obtener lo valores característicos y realiza la interpretación de estos valores del problema
http://www.guardarimagenes.com.ar/image/fotos/faf37a26f664af162053.png
1 respuesta
¿Lo qué está escrito a mano hay que hacerlo?
Es que en lo que tengo no habla de los valores característicos, yo solo tengo la
Unidad 2. Cadenas de Markov a tiempo discreto
Imagino que los valores característicos tienen que ver con los valores propios y vectores propios del Álgebra que los conozco, pero necesitaría o me vendría muy bien la teoría al respecto para las cadenas de Markov. Mira a ver si puedes hacerme llegar también los ejemplos que me mandaste un enlace a ellos pero no me funcionaba, puedes mandármelo por correo a [email protected] a dándome el enlace a una página de hosting donde lo cuelgues.
Pagina de apoyo
Considerando la presentación (ya veo que ya funciona)
http://www.slideshare.net/lupiuxlupiux/ejemplos-de-estacionalidad
Es que yo veo aquí dos problemas distintos. Lo que has escrito a mano y lo que está escaneado. No es que sea imposible, pero creo que nunca he visto un ejercicio donde se calculen valores propios de una matriz 4x4, por eso me extraña mucho y te pregunto si hay que hacer la primera parte, no me pongo a hacerla sin que me lo digas porque no se cómo será de complicado.
si hay que calcular los valores propios de la matriz de 4x4 y si hay que realizar la primera parte
saludos
Es que se trabaja muy mal con las x, t o lambdas para hacer ceros, por eso se resuelven hasta 3x3 donde hay una fórmula directa para calcular el determinante.
Bueno, pues calculemos los valores, usare la variable x para los valores propios
|P - x·Id | = 0
|-x 1/4 0 3/4|
|1/3 -x 0 2/3|
|1/2 0 -x 1/2| = 0
|1/2 0 1/2 -x |
A la segunda fila le sumamos la primera multiplicada por 4x
| -x 1/4 0 3/4 |
|1/3-4x^2 0 0 2/3+3x|
| 1/2 0 -x 1/2 | = 0
| 1/2 0 1/2 -x |
Ahora podemos desarrollar el determinante por la segunda columna que solo tiene un elemento no nulo. El determinante 4x4 será 0 si lo es el adjunto de 1/4
|1/3-4x^2 0 2/3+3x|
| 1/2 -x 1/2 | = 0
| 1/2 1/2 -x |
(1/3-4x^2)x^2 +(2/3+3x)(1/4) + (2/3+3x)(1/2)x -(1/3-4x^2)(1/4) = 0
x^2/3 - 4x^4 + 1/6 + 3x/4 + x/3 + 3x^2/2 - 1/12 + x^2 = 0
-4x^4 + x^2(1/3+3/2+1) + x(3/4+1/3) + 1/6 - 1/12 = 0
-4x^4 + (17/6)x^2 + (13/12)x + 1/12 = 0
48x^4 - 34x^2 - 13x - 1 = 0
Sabemos que por ser una matriz estocástica tiene el valor propio 1 seguro, lo cual podemos ver que es cierto
48 - 34 - 13 - 1 = 0
hacemos la división entre (x-1) por Ruffini
48 0 -34 -13 -1
1 48 48 14 1
-------------------
48 48 14 1 |0Queda 48x^3 + 48x^2 + 14x + 1 = 0
Y esto ya se escapa de lo habitual, haría falta un curso de teoría de ecuaciones para resolverlo.
Si hay alguna solución racional tendrá numerador 1 y denominador un divisor de 48
{1/2, -1/2, 1/3, -1/3, 1/4, -1/4, 1/6, -1/6, 1/8, -1/8, 1/12, -1/12, 1/16, -1/16, 1/24, -1/24}
Pero podría no servir ninguna de ellas.
Aparte hay métodos que te llevan a la respuesta sin tener que probar todos, pero no me acuerdo cómo son.
Bueno, que probando encontramos enseguida que -1/2 lo cumple
48(-1/8) +48(1/4) +14(-1/2) + 1 = -6 +12-7+1 = 0
Y calculamos el polinomio que queda al dividir por x+1/2
48 48 14 1
-1/2 -24 -12 -1
----------------
48 24 2 |048x^2 +24x +2 = 0
24x^2 + 12x +1 = 0
$$\begin{align}&x=\frac{-12\pm \sqrt{144-96}}{48}=\\ &\\ &\frac{-12\pm \sqrt{48}}{48}=\\ &\\ &\frac{-12\pm 4 \sqrt{3}}{48}\\ &\\ &\frac{-3\pm \sqrt{3}}{12}\\ &\\ &\text{Luego los valores propios son}\\ &\\ &\left\{1,\;-\frac 12,\;\frac{-3+ \sqrt{3}}{12},\;\frac{-3- \sqrt{3}}{12} \right\}\end{align}$$Esta es la gráfica de la cadena
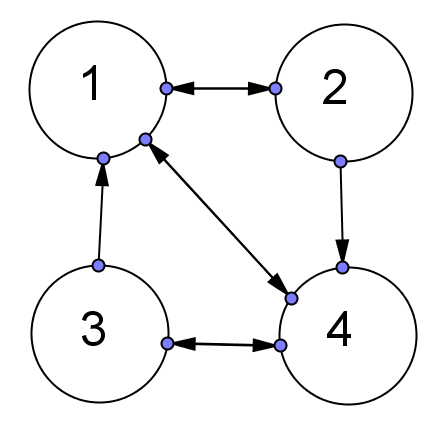
Tenemos el ciclo
1-->2-->4-->3-->1
Luego todos están comunicados, hay una sola clase y es una cadena irreducible
Todos los estados son recurrentes porque se puede regresar a todos ellos.
El periodo es 1 ya que para volver al 1 podemos dar dos pasos
1-->2-->1
o tres
1-->2-->4-->1
y el mcd(2,3)=1
Y todos los estados de la misma clase tienen el mismo periodo, luego todos tienen periodo 1 y la cadena es aperiódica.
Y eso es todo.
