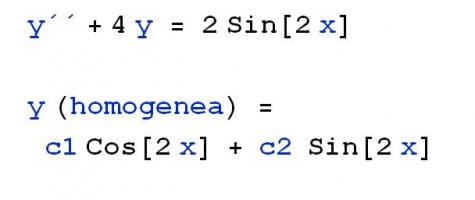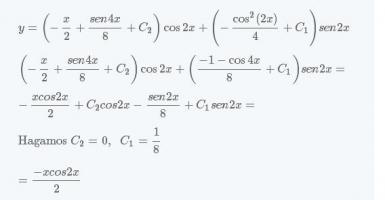Ecuación diferencial segundo orden

Calculo la solución general de la homogénea.

La ecuación característica es

k^2 + 4 = 0

k^2 = -4

k = +- 2i

Y cuando las raíces son complejas, son conjugadas de la forma

k1 = a+bi

k2 = a-bi

y las soluciones

y1= e^(ax)·cos(bx)

y2= e^(ax)·sen(bx

son independientes

y la solución general de la homogénea es

y = e^(ax)[C1·cos(bx)+C2·sen(bx)]

en nuestro caso a=0, b=2 y nos queda

y = C1·cos(2x) + C2·sen(2x)

Luego está bien la solución general de la homogénea que dabas.

Ahora la teoría dice que si sumamos a esta solución de la homogénea una solución particular de la no homogénea tendremos la solución general de la no homogénea.

Podemos usar el método de variación de las constantes. Haremos

y = A·y1+B·y2

con A y B funciones de x.

La teoría dice que debe cumplirse este sistema

$$\begin{align}&A´y_1+B´y_2= 0\\ &A´y_1´+B´y_2´= f(x)\\ &\\ &\\ &A´\cos 2x + B´sen 2x = 0\\ &-2A´sen2x+2B´\cos 2x = 2sen2x\\ &\\ &A´=-\frac{B´sen2x}{\cos 2x}\\ &\\ &\frac{2B´sen^2(2x)}{\cos 2x}+2B´\cos 2x= 2 sen2x\\ &\\ &2B'[sen^2(2x)+\cos^2(2x)]=2sen2x·\cos 2x\\ &\\ &B' = sen 2x·cos2x\\ &\\ &A´= \frac{-sen2x·\cos 2x·sen 2x}{\cos 2x}=-sen^2(2x)\\ &\\ &B=\int sen2x·cos2x dx = -\frac{\cos^2(2x)}{4}+C_1\\ &\\ &A=-\int sen^2(2x)dx = - \int \frac{1-\cos 4x}{2}dx=\\ &\\ &-\frac x2+\frac{sen4x}{8}+C_2\\ &\\ &\\ &y= \left(-\frac x2+\frac{sen4x}{8}+C_2\right)\cos 2x+\left(-\frac{\cos^2(2x)}{4}+C_1 \right)sen 2x =\\ &\\ &\left(-\frac x2+\frac{sen4x}{8}+C_2\right)\cos 2x+\left(\frac{-1-\cos 4x}{8}+C_1 \right)sen 2x =\\ &\\ &-\frac{xcos2x}{2}+C_2cos 2x-\frac{sen2x}{8}+C_1sen2x=\\ &\\ &\text{Hagamos }C_2= 0,\;\; C_1=\frac 18 \\ &\\ &\\ &=\frac{-xcos 2x}{2} \\ &\\ &\text{finalmente sumamos esta particular y la general homogénea}\\ &\\ &y = C_1cos 2x + C_2sen 2x -\frac {xcos2x}{2}\\ &\\ &y= \left(C_1-\frac x2\right)\cos 2x+C_2sen2x\\ &\\ &\\ &\end{align}$$

Y eso es todo, espero que te sirva y lo hayas entendido. Si no entendiste algún paso consúltamelo. Si la consulta va a ser algo menos sencillo mandala en otra pregunta por favor, que esta ya está bien currada.

Una aclaración, al despejar A´= -B´sen(2x) / cos(2x) no se si sera un error o es que yo no se sacarlo pero yo creo que debería ser A´= B´cos(2x) / sen(2x)

Corrígeme si estoy equivocado.

Gracias.

Perdón, ahora lo he visto claro. No hay fallo, era yo que estaba despejando la ecuación que no era.

Aquí creo que hay un error:

2B'[sen^2(2x)+cos^2(2x)]=2sen2x·cos2x

Porque si miras la linea anterior el cos^2(2x) no debería estar al cuadrado.

Corrígeme si me equivoco.

No, está todo perfecto. Con respecto a la línea anterior he multiplicado todos los términos por cos(2x) y he sacado factor común 2B'.

A lo mejor pensabas que pasaba cos(2x) al otro lado, pero eso no se puede hacer directamente, para pasarlo al otro lado debe ser denominador común de todo el primer miembro y para que eso sea así hay que multiplicar el termino que no lo tiene por cos(2x).

Por eso yo prefiero decir lo multiplico todo por cos(2x) en vez de decir hacemos la suma de fracciones poniendo denominador común y pasamos el denominador al otro lado. Es mucho más corto de expresar y sencillo de hacer.

Luego está bien. Y el resultado está comprobado q

Ue está bien también.

Me podrías indicar como has hecho la integral de B' ?? La has resuelto asi directamente o habría que hacerla por partes o por algún otro metodo?

No sabes lo que cuesta trabajar con el editor de ecuaciones. Cuando metes un desarrollo de más de 5 líneas complicadas el ordenador se pone lento que parece que se va a colgar y tienes miedo de que se pierda todo el trabajo que has hecho. Aparte de lo incomodo que es escribir las fórmulas sin métodos visuales tipo iconos. Por eso se ahorra lo que se puede cuando se usa. Entonces esa integral para alguien que me está pidiendo una ecuación diferencial de segundo orden me parece que es una cosa masticada y si no te sale hacerla mentalmente es fácil comprobar que está bien haciendo la derivada.

Con todos los pasos se haría con un cambio de variable

t = cos 2x

dt = - 2sen 2x dx ==> sen 2x dx =- dt/2

-$(t/2)dt = -(t^2)/4 + C = - cos^2(2x) + C1

Ahora que lo veo habría sido más fácil con el cambio

t = sen 2x

Y el resultado habría sido sen^2(2x) + K

Podría parecer que son dos respuestas distintas pero no lo son porque simplemente difieren en una constante

sen^2(2x) - (-cos^2(2x)) = 1

Y por lo tanto ambas son funciones primitivas de sen(2x)·cos(2x). A mi me salio esa porque no hice el cambio sino que vi que al derivar lo que pensé daba lo que tenía que dar.

Y eso es todo.

Perdona por pedirte tantas aclaraciones.

Pero cuando sacas esta solución particular:

Me podrías indicar que estas sustituyendo y de donde has sacado dicha función?

Es que no soy capaz de ver claro el procedimiento que has seguido después de obtener los valores de A y B.

Gracias.

Recuerda lo que te dije al terminar la pregunta inicial.

Y eso es todo, espero que te sirva y lo hayas entendido. Si no entendiste algún paso consúltamelo. Si la consulta va a ser algo menos sencillo mandala en otra pregunta por favor, que esta ya está bien currada.

Esta es la hora en la que he contestado una de las preguntas más difíciles que he contestado en toda mi trayectoria y aun estoy dando explicaiones de detalles menos importantes sin haber conseguido un solo punto. Yo creo que deberías darte cuenta del trabajo no ya solo extra sino super extra que me estás dando y puntuar la pregunta y continuar el curso a través de otras preguntas.