Ayuda con un problema de optimización no se como resolverlo
encontrar las dimensiones del rectángulo de área máxima que tiene su base en el eje OX y dos vértices en la curva definida por 4x^2+9y^2-36
1 respuesta
La curva 4x^2 + 9y^2 - 36 = 0 es una elipse centrada. Si la dibujas verás que el semieje X mide 3 y el semieje Y mide 2.
La elipse es simétrica respecto al eje Y, luego si el punto (x, y) pertenece a la elipse también pertenece el punto (-x, y). Luego si un vértice es (x, y) el otro es (-x, y)
Vamos a plantear una función que nos de el área del rectángulo en función del punto x del vértice derecho.
La coordenada y del vértice será
4x^2 + 9y^2 = 36
9y^2 = 36-4x^2
y^2 = (36-4x^2) / 9
y = sqrt(36-4x^2) / 3
Esta coordenada es la altura del rectángulo y la base es 2x, luego el área es
area(x) = 2x·sqrt(36-4x^2)/3 =(2/3)x·sqrt(36-4x^2)
derivaremos e igualaremos a 0 para calcular el máximo
$$\begin{align}&area ´(x) = \frac 23 \left(\sqrt{36-4x^2} +x·\frac{-8x}{2 \sqrt{36-4x^2}}\right)=0\\ &\\ &\frac{36-4x^2-4x^2}{\sqrt{36-4x^2}-4x^2}=0\\ &\\ &\\ &36-8x^2=0\\ &\\ &8x^2=36\\ &\\ &x^2=\frac{36}{8}= \frac 92\\ &\\ &x=\frac{3}{\sqrt 2 }\\ &\\ &Entonces\\ &\\ &base = 2x = \frac{2·3}{\sqrt 2}= 3 \sqrt 2\\ &\\ &atura = \frac{\sqrt{36-4x^2}}{3}=\frac{\sqrt 36-4·\frac 92}{3}=\sqrt 2\end{align}$$Esas son la dimensiones y el área máxima es 6.
Y eso es todo.
una duda la base porque sería 2x en vez de x? lo demás si lo tengo claro
Es por la simetría de la elipse y el rectángulo respecto del eje Y, la coordenada x indica la mitad de la base. Con el dibujo lo verás perfecto.
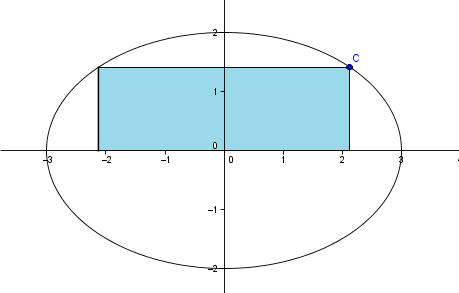
La solución del área máxima sería 12 no 6 por que se supone que es 4xy no 2xy por que la altura es 2y y la base 2x - Sebastian Tenesaca
No, el área máxima es 6, fíjate que el enunciado dice que la base está en el eje X, la altura es y no es 2y, es tal como en el didujo, donde puedes ver como es el rectángulo y verás que es imposible que pueda valer 12 el área. Saludos - Valero Angel Serrano Mercadal