Encuentra la ecuación general y en su forma canónica, de la hipérbola cuyo eje transversal es por=3

Hallamos los vértices de la elipse, para ello la ponemos en forma canónica completando cuadrados. He dicho que es elipse por la forma de la ecuación general

ax^2 + by^2 + ... con a, b mayores que cero

2(x^2-14x) + (y+4)^2 - 16 +108 = 0

2[(x-7)^2 - 49] + (y+4)^2 +92 = 0

2(x-7)^2 - 98 + (y+4)^2 +92= 0

2(x-7)^2 + (y+4)^2 = 6

(x-7)^2 / 3 + (y+4)^2 / 6 = 1

El semieje en X mide sqrt(3) y en Y mide sqrt(6)

Mide más en Y luego el eje transversal es paralelo a Y

El centro es (7, -4) Y los vértices de la elipse son

V1=(7, -4-sqrt(6))

V2=(7, -4+sqrt(6))

El centro de la circunferencia se halla completando cuadrados de igual forma. Y he dicho circunferencia porque x^2 e y^2 tienen el mismo coeficiente positivo que es 1

x²+y²-6x+4y+3=0

(x-3)^2 - 9 + (y+2)^2 - 4 + 3 = 0

El centro de la circunferencia es (3-2)

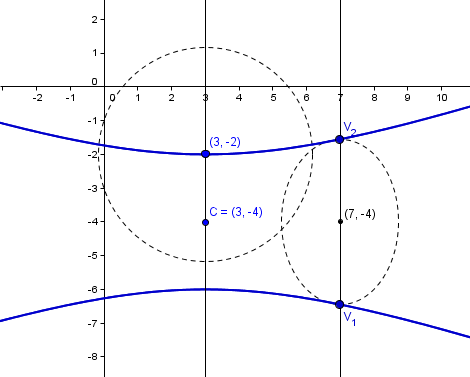
Al pasar la hipérbola por V1 y V2 que están en vertical, son simétricos respecto del eje perpendicular que pasa por el centro, luego la coordenada Y del centro de la hipérbola es -4, y como está en la recta x=3 tenemos que el centro de la hipérbola es (3, -4)

Y la ecuación será

(y+4)^2 / r - (x-3)^2 / s = 1

Hagamos que pase por el punto (3,-2)

(-2+4)^2 / r - (3-3)^2 / s = 1

4/r = 1

r= 4

Y ahora hagamos que pase por uno de los vértices de la elipse

(-4-sqrt(6)+4)^2 / 4 - (7-3)^2 /s = 1

6 / 4 - 16/s = 1

1/2 = 16/s

s=32

Y la ecuación canónica será

(y+4)^2 / 4 - (x-3)^2 / 32 = 1

o bien poniendo los denominadores como 2^2 y como (4sqrt(2))^2

Y la ecuación general será

8(y+4)^2 - (x-3)^2 = 32

8y^2 + 64y + 128 - x^2 + 6x - 9 = 32

8y^2 - x^2 + 64y +6x +87 = 0

Y eso es todo.