Desigualdades; Solución con notación de Intervalos

El producto de tres factores es estrictamente negativo cuando los tres son estricetamente negativos o cuando dos son estrictamente positivos y uno estrictamente negativo.

2x+3 < 0 <==> 2x < -3 <==> x < -3/2

Todos los pasos son si y solo si, luego del final se deduce el inicio

Cuando x < -3/2 el factor 2x+3 será negativo

Y de igual forma se comprueba que

Cuando x > -3/2 el factor 2x+3 es positivo

1 - 3x < 0 <==> 1 < 3x <==> 3x > 1 <==> x > 1/3

Luego si x > 1/3 tenemos 1-3x < 0

Y se puede comporbar que si x < 1/3 tenemos 1-3x > 0

Y el último es el más sencillo

x-2 < 0 <==> x < 2

sI x < 2 se cumple x-2 negativo y si x > 2 se cumple x-2 > 0

Bueno, para que el producto sea negativo han de ser tres los tres factores negativos o ninguno. Pondremos las desigualdades que se dan en cada uno de esos casos, es un poco lioso pero con cuidado se hace.

1) Los tres negativos

x<-3/2, x>1/3, x<2

Es imposible porque para x<-3/2 sería negativo y para x>1/3 sería positivo imposible ser positivo y negativo a la vez

2) Primero negativo y los otros dos positivos

x<-3/2, x<1/3, x>2

Es imposible, por la primera es negativo pero por la última es positiva

3) Segundo negativo y los otros positivos

x >-3/2, x>1/3, x>2

Sirve, basta con que sea x>2

4) Tercero negativo y los otros positivos

x>-3/2, x <1/3, x<2

sirve, la solución es (-3/2, 1/3)

Luego la solución es la unión de los casos tercero y cuarto.

Solución = (-3/2, 1/3) U (2, +infinito)

La verdad es que me ha venido justo para enterderme a mi mismo, será mejor hacerlo gráficamente. En rojo he puesto la zona donde los factores son negativos. Y la respuesta es donde coinciden los tres en rojo o solo hay uno en rojo.

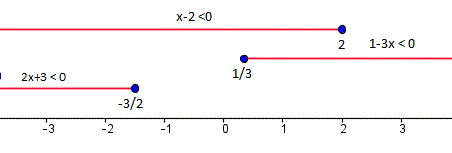
por lo tanto la respuesta es

(-3/2, 1/3) U (2, +infinito)

Y eso es todo.