¡Trabajo en una pista semicircular!
Hola valeroasm! :) Espero puedas responder mi pregunta:
Tengo una pista semicircular sin roce de radio R=(raíz de 3) metros. Una partícula de masa M=2(raíz de 3)Kg se mueve apoyada sobre la pista. Sobre ella actúan, ademas de la gravedad y la fuerza de contacto, una fuerza constante S horizontal hacia la derecha de 14Newtons.
¿Cuál el trabajo de cada fuerza sobre la partícula cuando se mueve del punto A al B?
Además si la rapidez en el punto A es de 4m/s ¿Cuanto vale la rapidez en el punto B y el modulo de la normal en ese punto?, esto, sin olvidar la fuerza S. 
Me seria de ayuda tu respuesta! De antemano, gracias! Un Saludo.
1 Respuesta
¡Hola!
Si! Tenia la curiosidad de saber el procedimiento que seguías, ya que como también está toda la teoría de energía, quería ver que camino seguir, pero así esta bien, ¡muchas gracias por la respuesta! Saludos :)
Si, pero yo no soy muy experto en Física. La teoría de las energías sirve para las fuerzas conservativas, como la gravedad por ejemplo. Pero las otras dos no lo sé. Precisamente la forma de saber si una fuerza es conservativa es calculando la integral cerrada en línea y viendo que es 0 o comprobando que la integral en línea es indistinta del camino.
Dame un poco de tiempo para terminarlo.
Daremos una parametrización del camino. Suponiendo que la circunferencia tiene el centro en (0,0) la parametrización es
f(t) = (sqrt(3)·cos(2Pi-t), sqrt(3)·sen(2pi-t)) con t€[0, 2pi/3]
ya que el ángulo recorrido es 120º=2pi/3
El campo de fuerzas de S es (14,0)
Y el trabajo realizado es
$$\begin{align}&T_S=\int_A^B S_xdx+S_ydy =\\ &\\ &\int_0^{2\pi/3}14 \sqrt 3 sen(2\pi-t)dt=\\ &\\ &14 \sqrt 3 \left[\cos(2\pi-t)\right]_0^{2\pi/3}=\\ &\\ &14 \sqrt 3(\cos(4\pi/3)- \cos(2\pi)]=\\ &\\ &14 \sqrt 3 \left(-\frac 12-1 \right)=-21 \sqrt 3 \;J\end{align}$$A posteriori me doy cuenta que es una fuerza conservativa, es como la gravedad pero puesta en el eje X. Y el trabajo ha sido la intensidad de la fuerza multiplicada por el espacio recorrido en el eje X
La fuerza de la gravedad efectúa un trabajo de mgh donde g = -9.8 y h tiene signo dependiendo de hacia donde ha sido el movimiento. En este caso
h=-sqrt(3)·cos30º
T_g = 2·sqrt(3) · (-9.8) · (-sqrt(3)·sqrt(3)/2) = 29.4·sqrt(3) J
La fuerza de contacto es normal al punto de contacto, está dirigida hacia el centro de la circunferencia.
En un momento dado sobre la partícula actúan tres fuerzas, la gravedad, la fuerza S y la de contacto.
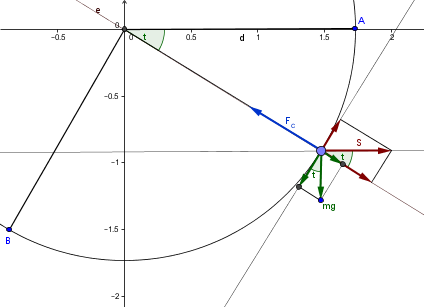
En el eje perpendicular a la trayectoria no hay movimiento, luego el sumatorio sde fuerzas es cero
|Fc| = -mg·sent + S·cost
|Fc| = 9.8·2·sqrt(3)·sent + 14cost = 19.6sqrt(3)·sen(t) + 14cost
Fc = (|Fc|cos(180º-t) , |Fc|sent) = (-|Fc|cost , |Fc|sent)
$$\begin{align}&T_{F_c}=\int_A^BF_{c_x}dx+F_{c_y}dy=\\ &\\ &\int_0^{2\pi/3}\{-(19.6 \sqrt 3sent+14cost)cost[\sqrt 3 sen(2\pi-t)]+\\ &\\ &(19.6 \sqrt 3sent+14cost)sent[-\sqrt 3 \cos(2\pi-t)]\}dt=\\ &\\ &\int_0^{2\pi/3}\left[(-58.8sent\,cost-14 \sqrt 3 \cos^2t)(-sent)+\right.\\ &\left.(-58.8sen^2t-14 \sqrt 3 sent\,cost)cost\right]dt=\\ &\\ &\\ &\int_0^{2\pi/3}(58.8sen^2t\,cost+14 \sqrt 3cos^2t\,sent-\\ &\\ &58.8sen^2t\,cost-14 \sqrt 3cos^2t\,sent) dt =\\ &\\ &\int_0^{2\pi3}0dt = 0\end{align}$$¡Bueno! Después de todo el tiempo que he usado me sale esto. Ya no se si es que he hecho algo mal o es lo que tenía que salir. Puede que algún teorema de Física diga que el trabajo de esa fuerza es nulo. Yo poco puedo decir sobre eso, he hecho el planteamiento matemático y me he liado bastante, pero creo que el resultado es 0.
Y suponiendo que el trabajo de la fuerza de contacto esté bien calculado tendríamos que el incremento de trabajo es igual al incremento de la energía cinética. No sé si empleáis la letra T o la W para el trabajo. Nosotros empleábamos la T pero ahora en todo lo que veo se usa la W.
W = EcB - EcA
donde EcB es la energía cinética en B y EcA la energía cinética en A
$$\begin{align}&-21 \sqrt 3 + 29.4 \sqrt 3 = \frac 12 mv^2 - \frac 12 m·16\\ &\\ &8.4 \sqrt 3+\frac 122 \sqrt 3·16=\frac 12 2 \sqrt 3\,v^2\\ &\\ &24.4 \sqrt 3 = \sqrt 3 v^2\\ &\\ &v^2= 24.4\\ &\\ &v= \sqrt{24.4}=4.9396356 m/s\end{align}$$Y el módulo de la normal en el punto B lo calculamos con la fórmula que ya deducimos antes
$$\begin{align}&|Fc| = 19.6 \sqrt 3·sen t + 14cost =\\ &\\ &\text{donde t = }=\frac{2\pi}{3}=120º\\ &\\ &= 19.6 \sqrt 3·\frac{\sqrt 3}{2}+14\left(-\frac 12\right)=\\ &\\ &9.8-7 = 2.8N\\ & \end{align}$$¡Uff! Casi no termino. Pon en cuarentena y revisa todo lo que hice ya que no soy experto en Física y lo que hice me costó bastante.
¡Tonto de mí!
Seguramente he hecho cosas que a lo mejor no has estudiado. El trabajo de la fuerza de contacto es 0 y se demuestra mucho más fácilmente porque en todo momento la fuerza es perpendicular a la trayectoria, por lo cual el producto escalar de la fuerza por el diferencial de desplazamiento es 0 y la integral de todos estos productos escalares infinitesimales es 0.
Y cuando el campo de una fuerza es constante en sus dos ejes el trabajo es la suma del producto de cada constante de cada eje por el respectivo espacio recorrido (con signo) en cada eje
$$\begin{align}&\int_A^BF·ds=\int_{A_x}^{B_x}F_xdx+\int_{A_y}^{B_y}F_ydy=\\ &\\ &Como\; F(C_1,C_2)\\ &\\ &=C_1\int_{A_x}^{B_x}dx+C_2\int_{A_y}^{B_y}dy=\\ &\\ &C_1(B_x-A_x)+C_2(B_y-A_y)\end{align}$$Y de esto se deduce en particular que las fuerzas que solo son verticales u horizontales son el producto de la fuerza (con signo) por el espacio recorrido (con signo) vertical u horizontalmente.
De aho se deduce que el trabajo de la fuerza S era
14· (-sqrt(3)/2- sqrt(3)) = -14 ·sqrt(3)(1+1/2) = -21sqrt(3).
Bueno, a veces es muy difícil contestar una pregunta sin saber el nivel de estudios del que procede la pregunta.
