Los cambios de varias variables ya son materia superior. Voy a intentarlo
$$\begin{align}&u=xy\\ &v=\frac yx\\ &\\ &\frac uv =\frac{xy}{\frac yx}=x^2\implies x=\sqrt {\frac uv}\\ &\\ &uv= xy \frac yx=y^2\implies y=\sqrt{uv}\\ &\\ &\end{align}$$$$I=\begin{vmatrix}
\frac{\partial x}{\partial u}&\frac{\partial x}{\partial v}\\
\frac{\partial y}{\partial u}&\frac{\partial y}{\partial v}
\end{vmatrix}=
\begin{vmatrix}
\frac{1}{2 \sqrt{uv}}&\frac{-\sqrt u}{2v \sqrt v}\\
\frac{\sqrt v}{2 \sqrt u}&\frac{\sqrt u}{2 \sqrt v}
\end{vmatrix}=
\\
=\frac{\sqrt u}{4v \sqrt u}+\frac{\sqrt {uv}}{4v \sqrt{uv}}=\frac{1}{4v}+\frac{1}{4v}=\frac {1}{2v}$$Y ahora vamos a cambiar los limites de integración.
Trasformamos las funciones de x,y que limitaban el recinto a funciones de u,v
$$\begin{align}&y=\frac 1x\implies \sqrt{uv}=\frac{1}{\sqrt{\frac uv}}\implies u=1\\ &\\ &y=x \implies \sqrt{uv}=\sqrt{\frac uv}\implies v=1\\ &\\ &y=2x \implies \sqrt{uv}=2 \sqrt{\frac uv}\implies v=2\\ &\\ &x=\sqrt 2 \implies \sqrt{\frac uv}= \sqrt 2 \implies v=\frac u2\end{align}$$Primero voy a presentar la equivalencia con el dominio anterior pintando las funciones y areas con el mismo color
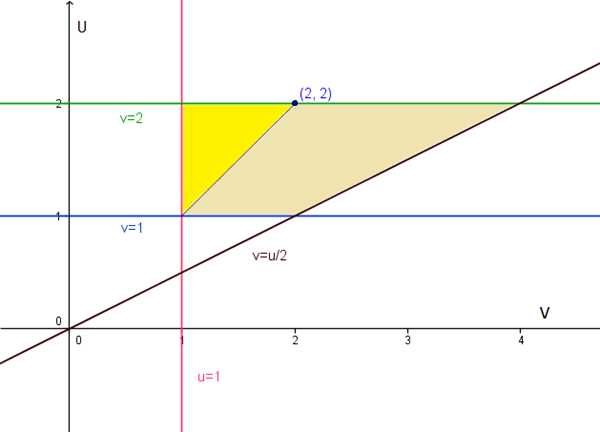
Vaya, podría haber puesto los ejes al reves y se vería mejor que se puede hacer todo en una integral. De todas formas se puede hacer, tomaremos la v como variabole independiente, asi la función que hace de límite de integración en vez de v=u/2 será u=2v. Estos son los límites del dominio tomado todo de una vez
v € [1,2]
u € [1, 2v]
$$\begin{align}&4\iint_R \frac{\cos\left(\frac{\pi y}{2x}\right)y^2e^{x^2y^2}}{e^{\frac{4y^2}{x^2}}-e}=\\ &\\ &u=xy \quad\quad v=\frac yx\quad \quad x^2=\frac uv \quad\quad y^2=uv\\ &\\ &Jacobiano = \frac{1}{2v}\\ &\\ &\\ &4\int_1^2\int_1^{2v} \;\;\frac{\cos \left(\frac{\pi v}{2}\right)u v e^{u^2}}{e^{4v^2}-e}·\frac{1}{2v}dudv =\\ &\\ &\int_1^2 \frac{\cos \left(\frac{\pi v}{2}\right)}{e^{4v^2}-e}\int_1^{2v}2ue^{u^2}dudv=\\ &\\ &\int_1^2 \frac{\cos \left(\frac{\pi v}{2}\right)}{e^{4v^2}-e}\left[e^{u^2} \right]_1^{2v}dv=\\ &\\ &\int_1^2 \frac{\cos \left(\frac{\pi v}{2}\right)}{e^{4v^2}-e}\left(e^{4v^2}-e \right)dv=\\ &\\ &\\ &\int_1^2 \cos \left(\frac{\pi v}{2}\right)dv=\left. \frac{2}{\pi}sen \left(\frac{\pi v}{2}\right)\right|_1^2=\\ &\\ &\frac{2}{\pi}\left[sen\pi-sen\left(\frac{\pi}{2}\right)\right]=\frac{2}{\pi}(0-1)=-\frac{2}{\pi}\\ &\\ &\end{align}$$¡Uff, por fin!
En vez de sutituir y^2 por uv puse u/v y no había forma de sacarla, incluso hice un programa de integración númerica en el ordenador que me decía que la respuesta que decías era verdadera, luego tenia que llegar a ella. Hasta que no me di cuenta de ese fallo han pasado horas.
Y eso es todo.



