Sea ABCDEF el hexágono formado por 6 rectas tangentes de una cónica,

a) Como la excentricidad es menor de 1 se trata de una elipse. Y por las coordenadas que nos dan de los vértices, estos determinan que el eje transversal es y=7 que es paralelo al eje X, luego el semieje mayor es paralelo al eje X. Eso tiene su importancia en la ecuación canónica porque el cociente de x² será mayor que el de y².
Y también nos determinan el centro de la elipse que es el punto intermedio entre ambos
centro = ((-2+8)/2, (7+7)/2) = (3, 7)
El semieje mayor será a= d((3,7),(8,7)) = 5
Con todo esto, la ecuación canónica será:

$$\frac{(x-3)^2}{25}+ \frac{(y-7)^2}{b²}=1$$

Sabemos que la excentricidad es c/a = 4/5 luego
c=4a/5 = 4·5/5 = 4
Y sabemos que a² = b²+c², luego b² = a²-c² = 25 - 16 = 9

$$\begin{align}&\text {y la ecuación de la elipse será}:\\ &\\ &\frac{(x-3)^2}{25}+ \frac{(y-7)²}{9}= 1\end{align}$$

La gráfica irá después con todo.
b) Como ayuda para el cálculo de los puntos con una abcisa dada vamos a despejar la y

$$\begin{align}&\frac{(x-3)^2}{25}+ \frac{(y-7)^2}{9}= 1\\ &\\ &\\ &\frac{(y-7)^2}{9}=1- \frac{(x-3)^2}{25} = \frac{25-(x-3)^2}{25}\\ &\\ &\\ &y = 7 \pm \frac 35 \sqrt{25-(x-3)^2}\\ &\\ &\\ &x= 0\implies\\ &y=7\pm \frac 35· 4= \frac{47}{5} y \frac{23}{5}=9.4 \;y \;4.6\\ &\\ &\\ &x=4 \implies\\ &y = 7\pm \frac 35 \sqrt{24}\approx 9.939387691 \;y\;4.060612309\\ &\\ &\\ &x=7 \implies\\ &y = 7 \pm \frac 35 ·3 =\frac{44}{5} y \frac{26}{5}=8.8 \;y \;5.2\end{align}$$

Esta es la imagen:

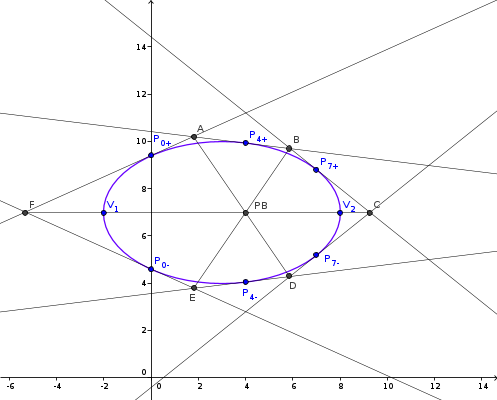
c) Para hallar la ecuación de las rectas tangentes en un punto dado, no se me ocurre nada mejor que calcular la pendiente mediante la derivada de la función en el punto y usar una formulilla.
La derivada es:

$$\begin{align}&y=7 \pm \frac 35 \sqrt{25-(x-3)^2}\\ &\\ &\\ &y'= \mp \frac{3(x-3)}{5· \sqrt{25-(x-3)^2}}\\ &\\ &\\ &\text{La notación 0+ significa punto 0 rama superior}\\ &\text{de la elipse. 0- para la rama inferior}\\ &\\ &y'(0+)=-3(-3)/5·4=9/20\\ &y'(4+)=-3(4-3)/5 \sqrt{24}=-\sqrt 6/20\\ &y'(7+)=-3(7-3)/5·3 =-4/5\\ &y'(7-) =4/5\\ &y'(4-)= \sqrt 6 / 20\\ &y'(0-)=-9/20\end{align}$$

Hemos calculado las derivadas en el orden circular de los puntos.
Las ecuaciones de las rectas podrían darse en forma paramétrica o vectorial sin hacer casi cuentas, pero me he dado cuenta que luego no hay quien halle las intersecciones.
Dado un punto (x0, y0) y una pendiente m la ecuación de la recta que pasa por ese punto y tiene esa pendiente es.

$$\begin{align}&y= y_0 +m(x-x_0)\\ &\\ &r_{0+}:\; y=\frac{47}{5}+\frac{9}{20}x=\frac{188+9x}{20}\\ &\\ &\\ &\\ &\\ &\\ &r_{4+}:\; y = 7+\frac{6 \sqrt 6}{5}-\frac{(x-4) \sqrt 6}{20}\\ &\\ &r_{4+}:\; y=\frac{140+28 \sqrt 6-x \sqrt 6}{20}\\ &\\ &\\ &\\ &\\ &\\ &r_{7+}:\;  y=\frac {44-4(x-7)}{5}=\frac{72-4x}{5}\\ &\\ &\\ &\\ &\\ &\\ &r_{7-}:\; y=\frac{26}{5} +\frac {4(x-7)}{5}=\frac{-2+4x}{5}\\ &\\ &\\ &\\ &\\ &r_{4-}:\; y = 7-\frac{6 \sqrt 6}{5}+\frac{(x-4) \sqrt 6}{20}\\ &\\ &r_{4-}:\; y =\frac{140-28 \sqrt 6+ x \sqrt 6}{20}\\ &\\ &\\ &\\ &\\ &r_{0-}:\; y=\frac{23}{5}-\frac{9}{20}x=\frac{92-9x}{20}\end{align}$$

Ahora toca hacer la intersección de cada recta con la siguiente, casi nada.
Igualaré las expresiones de de las rectas y a despejar

$$\begin{align}&188+9x=140+28 \sqrt 6 -x \sqrt 6\\ &\\ &x =\frac{-48+28 \sqrt 6}{9+ \sqrt 6}=-8+4 \sqrt 6\approx 1.797958971\\ &\\ &y =\frac{188+9(-8+4 \sqrt 6)}{20}=\frac{29+9 \sqrt 6}{5}\approx 10.209008154\\ &\\ &\text {acabamos de encontrar el punto A}\\ &\\ &\\ &140+28 \sqrt 6 - x \sqrt 6=288-16x\\ &\\ &x=\frac{148-28 \sqrt 6}{16- \sqrt 6}=\frac{44-6 \sqrt 6}{5} \approx 5.860612309\\ &\\ &\\ &y=\frac{72-4 \left ( \frac{44-6 \sqrt 6}{5} \right)}{5}=\frac{184+24 \sqrt 6}{25} \approx 9.711510153\\ &\\ &\text{Ese es el punto B}\\ &\\ &\\ &72-4x=-2+4x\\ &\\ &x=74/8 =37/4 = 9.25\\ &\\ &y=\frac{72-37}{5}= 7\\ &\\ &\text{Ese era el punto C}\\ &\\ &\\ &\text{El punto D es simetrico de B respecto a la recta y=7}\\ &\text{entre las dos coordenadas de y deben sumar 14}\\ &\\ &x=\frac{44-6 \sqrt 6}{5} \approx 5.860612309\\ &y=\frac{166-24 \sqrt 6}{25} \approx 4.288489847\\ &\\ &\text{Ese era el punto D}\\ &\\ &\\ &\text{El punto E es simetrico de A respecto y=7}\\ &\\ &x =8+4 \sqrt 6\approx 1.797958971\\ &\\ &y =\frac{41-9 \sqrt 6}{5}\approx 3.790918463\\ &\\ &\text{Ese era el punto E}\\ &\\ &\\ &188+9x=92-9x\\ &\\ &x=\frac{-96}{18}=-\frac{16}{3}\approx-5.33333333...\\ &\\ &y = \frac{188-9·\frac{16}{3}}{20}=\frac{3·188-9·16}{60}=\frac{420}{60}=7\\ &\\ &\text{Y ya está el punto F}\end{align}$$

Ufff, ufff, Ufff!
Llevo varias horas, porque te equivocas de vez en cuando y hay que corregir y porque el editor este va fatal cuando introduces muchas líneas. No sé si este último bloque de lineas se verá bien por eso mismo.
Aun queda la parte final, pero la página está tan cargada que se paraliza y es imposible trabajar, es necesario continuar en una pregunta nueva.

Por favor puntúa ya y vuélvela a mandar, que este trabajo merecería los puntos de 10 preguntas comunes. Vuélvela a mandar porque yo no puedo contestar cuando quiero sino cuando me mandan pregunta. Y mandámela a mi.