Problema de la ecuación general de segundo grado. Geometría analítica I

En la primera parte, la de la hipérbola no me aparece por dónde pasa la hipérbola. Escríbelo de nuevo, si fue con el editor de ecuaciones asegurate después que se ha mandado correctamente.

Buenas noches.
Necesito apoyo. Gracias y saludos.
Problema de la ecuación general de segundo grado.

Encuentra la ecuación, general y en su forma canónica, de la hipérbola cuyo eje transversal es x = 3 y que pasa por: Los vértices de la cónica 2x² + y² - 28x + 8y + 108=0 y El centro de la cónica x² + y² - 6x + 4y + 3 = 0

Encuentra a qué cónica pertenece cada una de las ecuaciones generales de este problema. Argumenta tu respuesta.

Es que pensaba que lo de los vértices y centro de las otras cónicas eran problemas aparte.

Primero vamos a expresar la ecuación de la hipérbola. Si el centro es (h, k) y el eje transversal es vertical la ecuación será.

$$\begin{align}&\frac{(y-k)^2}{a^2}-\frac{(x-h)^2}{b^2}= 1\\ &\\ &\text {Por ser x=3 el eje, el centro tendrá coordenada h=3}\\ &\\ &\frac{(y-k)^2}{a^2}-\frac{(x-3)^2}{b^2}= 1\end{align}$$

Tenemos tres incógnitas k, a y b. Que intentaremos despejar con las otras condiciones. No conozco las fórmulas para el cálculo rápido de vértices, focos y otros elementos, pero todo puede hacerse.

2x² + y² - 28x + 8y + 108=0 es una elipse no inclinada por suerte por no tener el temible termino en xy

Completamos cuadrados

$$\begin{align}&2(x-7)^2-98+(y+4)^2-16+108 = 0\\ &\\ &2(x-7)^2 + (y+4)^2 = 6\\ &\\ &\frac{(x-7)^2}{(\sqrt 3)^2}+ \frac{(y+4)^2}{(\sqrt 6)^2} = 1\\ &\end{align}$$

El semieje en X es raíz de 3 y en Y es raíz de 6. Como es mayor en Y, la elipse tiene el eje transversal en sentido vertical. Los vértices serán la intersección d ela elipse con la recta vertical pasando por el centro

Esa recta es x = 7

Si en la ecuación de la recta sustituimos x = 7 no cuesta nada encontrar que y puede tomar los valores:

$$\begin{align}&y_1=\sqrt 6 -4\\ &y_2=-\sqrt 6-4\\ &\\ &\text {Luego los vértices de la elipse son}:\\ &\\ &(7,\sqrt 6 -4)\\ &(7,-\sqrt 6 - 4)\end{align}$$

Lo dejo momentáneamente, tengo que hacer otras cosas. Después volveré.

Si acaso me dices si lo vas entendiendo.

Y la ecuación

x² + y² - 6x + 4y + 3 = 0

Es la de una circunferencia, completamos cuadrados para hallar el centro que nos piden

(x-3)² -9 +(y+2)²-4+3 = 0

Luego el centro es (3,-2)

Ya tenemos los tres puntos por donde debe pasar la hipérbola, ahora los sustituiríamos y tendríamos 3 ecuaciones.

Pero antes de nada fíjate en los dos vértices de la elipse por los que pasa la hipérbola, están en una línea vertical paralela el eje de la hipérbola. La perpendicular a ese eje pasando por el centro es eje de simetría de las dos hojas. Eso quiere decir que el centro de la hipérbola está a igual distancia de los vértices d ela elipse y por lo tanto siu coordenada y es

$$\frac{-4+\sqrt 6 - 4-\sqrt 6}{2}=-4$$

Luego el centro de la hipérbola es (3,-4)

Y su ecuación ya queda reducida a:

$$\begin{align}&\frac{(y+4)^2}{a^2}-\frac{(x-3)^2}{b^2}= 1\\ &\\ &\\ &(y+4)^2b^2-(x-3)^2a^2 = a^2b^2\end{align}$$

De los tres puntos que tenemos sobra uno para hacer cuentas porque solo quedan dos incógnitas. Tomemos los puntos:

$$\begin{align}&(3,-2)\\ &(7,-4+\sqrt 6)\\ &\\ &(2)^2b^2-(0)^2a^2 = a^2b^2\\ &\\ &4b^2=a^2b^2\\ &\\ &a^2=4\\ &\\ &\\ &(\sqrt 6)^2b^2 -(-4)^2·4=4b^2\\ &\\ &6b^2-64 = 4b^2\\ &\\ &2b^2 = 64\\ &\\ &b^2 = 32\end{align}$$

Y después de todas estas cuentas es de suponer, si están bien hechas, que la ecuación general de la hipérbola será:

$$\begin{align}&(y+4)^2b^2-(x-3)^2a^2 - a^2b^2 = 0\\ &\\ &(y^2+16+8y)32 -(x^2+9-6x)4 -128 = 0\\ &\\ &-4x^2+32y^2+24x+256y +512-36-128 =0\\ &\\ &x^2 -8y^2 - 6x -64y -87 = 0\end{align}$$

Mientras que la canónica será

$$\frac{(y+4)^2}{4}+\frac{(x-3)^2}{32}= 1$$

Y he comprobado que está bien gráficamente.

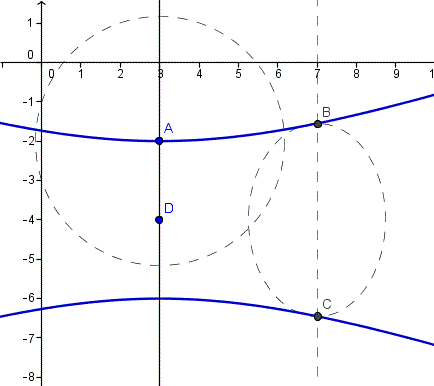
Y respecto a qué cónica correspondía a cada ecuación general tenemos.

La solución es una hipérbola porque así nos lo decía el enunciado. Bueno, y porque la x^2 y la y^2 tiene coeficientes de signo distinto.

2x² + y² - 28x + 8y + 108=0

es una elipse porque x^2 e y^2 tienen coeficientes de igual signo pero distintos

x² + y² - 6x + 4y + 3 = 0

En una circunferencia porque los coeficientes de x^2 e y^2 son iguales.

Y eso es todo.