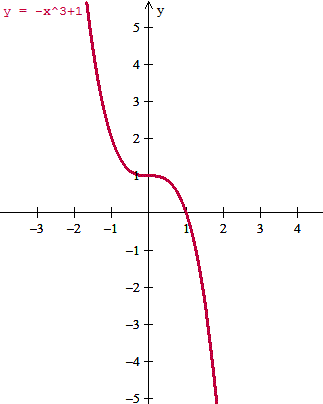Dominio de la función y gráfico además si esta dentro de los IR y si es función o no
$$\begin{align}&f(x)=(x³-a²x)/(a²-1)+1\end{align}$$indicar el valor de
A Î IR ( si existe )tal que la función sea uno a uno/ graficar
Determinar su dominio
Si a=x la expresión que resulta es una funcion.
Ayúdeme no entiendo matemáticas
1 respuesta
La función es continua ya que va a salir un simple polinomio cuando le demos un valor a a.
Una función continua es uno a uno si es siempre cereciente o siempre decreciente, para ello el signo de la derivada debe ser constante.
Calculémosla
$$\begin{align}&f(x)=\frac{x^3-a^2x}{a^2-1}+1\\ &\\ &f'(x)=\frac{3x^2-a^2}{a^2-1}\end{align}$$Espera, que esto no es fácil, dime el enunciado exacto, es que no está claro.
Que te pide, encontrar un valor de a tal que la función sea uno a uno
O encontrar un intervalo de R tal que la función sea uno a uno
Es que esto que pusiste no se entiende
A Î IR
Espero la aclaración, pero ahora tengo que irme y hasta unas horas no volveré.
Pide indicar el valor de a si pertenece o no a IR (no puedo hacer el sigo pertenece) tal que la función sea uno a uno ( si existe) y hacer un gráfico.
Determinar su dominio.
si a=x ¿La expresión resultante es una función?.
$$\begin{align}&f'(x)=\frac{3x^2-a^2}{a^2-1}=0\\ & Supondremos\, que\quad a^2-1 \neq 0\\ & \\ & 3x^2 - a^2 = 0\\ & \\ & 3x^2=a^2\\ &\\ &x =\pm \frac{a}{\sqrt 3}\\ &\\ &\text {para que solo haya un corte debe ser a=0}\end{align}$$Luego la función será uno a uno en todo R cuando a=0 y queda
f(x) = (x^3-0) /(0-1) + 1
f(x) = -x^3 + 1
y la gráfica es:
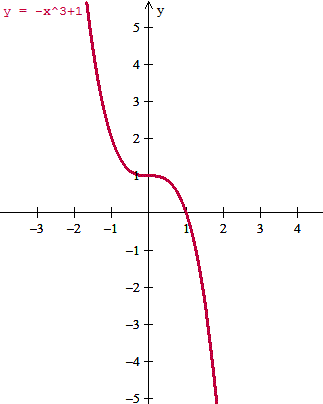
El dominio es todo R, y en todo R es uno a uno porque es monótona decreciente en todo momento.
Si sustituimos a por x quedará
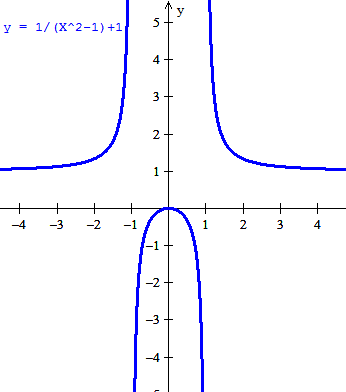
$$\begin{align}&f(x)=\frac{x^3-a^2x}{a^2-1}+1\\ &\\ &f(x)=\frac{x^3-x^3}{x^2-1}+1= \frac{1}{x^2-1}+1\end{align}$$Y lo que resulta es una función definida en todo R salvo en los puntos -1 y 1.
Y no es uno a uno ya que f(x) = f(-x) por lo que siempre hay al menos dos puntos con el mismo valor salvo quizá para x=0
Esta es la gráfica.
Y esto es todo, espero que te sirva y lo hayas entendido. Si no es así pregúntame, y si ya está bien no olvides puntuar.
Un saludo
-------------------------
Unas palabras para el supervisor. He tenido algunos problemas con el editor o no sé que pasado que la caja de ecuaciones se puso ella sola al comienzo por delante del texto que tenía y era imposible borrarla y volverla a escribir debajo, falta el botón de borrar cajas de ecuaciones. No he usado el sistema de insertar gráficos nuevo porque no tiene la posibilidad de visión y recuperación de imágenes, al menos de momento. Muchas veces seleccionaba todo con CTRL+A y lo copiaba con CTRL+C por si había un fallo al mandar la respuesta.
Ahora al seleccionar esta página con CTRL+A no se seleccionaba todo, solo hasta el final del primer gráfico.
