Área de Superficies de revolución

Lugui Bogo!

Hagamos la gráfica para enterarnos.

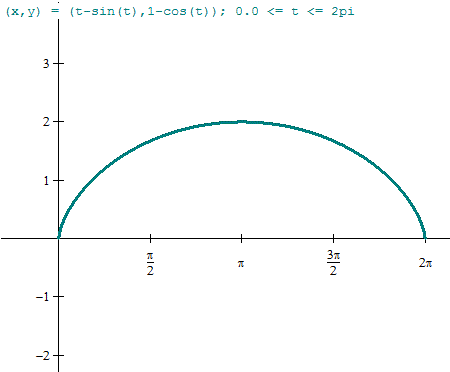
Pues el problema es que no es muy conocida (si existe) la fórmula para calcular el volumen de un sólido de revolución a partir de las ecuaciones paramétricas de la función que gira.

Luego creo que no habrá otro remedio que transformar en coordenadas cartesianas

x=t-sent

y=1-cost

Y aquí no se puede despejar la y como función de x

y=f(x)

la x si se puede despejar como función de y, pero eso no nos sirve.

Pues tendré que deducir la fórmula para ecuaciones paramétricas.

$$\begin{align}&V=\pi\int_{x_0}^{x_1}[f(x)]^2dx=\\ &\\ &\text{dividimos en intervalo en n trozos}\\ &\Delta x=\frac{x_1-x_0}{n}\\ &\\ &V=\pi\lim_{n\to \infty} \sum_{i=0}^{n-1}[f(x_0+i·\Delta x)]^2·\Delta x\\ &\\ &\text{Si dividimos el intervalo de tiempo en trozos}\\ &\\ &\Delta t = \frac{t_1-t_0}{n}\\ &\\ &V=\pi \lim_{n\to \infty}\sum_{n=0}^{n-1}[y(t_0+i·\Delta t)]^2·[x(t_o+(i+1)\Delta t)-x(t_0+i\Delta t)]\\ &\\ &\text{multiplicando y dividiendo por }\Delta t\\ &\\ &V=\pi \lim_{n\to \infty}\sum_{n=0}^{n-1}[y(t_0+i·\Delta t)]^2·\frac{x(t_o+(i+1)\Delta t)-x(t_0+i\Delta t)}{\Delta t}·\Delta t\\ &\\ &\text{El límite de ese cociente es la derivada en } t_0+i\Delta t\\ &\text{con lo cual queda}\\ &\\ &V=\pi \int_{t_0}^{t_1}[y(t)]^2·x'(t)\;dt\\ &\\ &\text{Y en este caso será}\end{align}$$

$$\begin{align}&V=\pi\int_0^{2\pi}(1-\cos t)^2(1-cost)dt=\\ &\\ &\pi\int_0^{2\pi}(1-3cost+3cos^2t-\cos^3t)dt=\\ &\\ &\pi\left[t -3sent\right]_0^{2\pi}+\\ &\\ &\pi\int_0^{2\pi}\left(\frac{3}{2}+\frac{3cos 2t}{2}-(1-sen^2t)cost \right)dt=\\ &\\ &2\pi^2+\pi\left[\frac{3t}{2}+\frac{3sen 2t}{4}-sent  \right]_0^{2\pi}+\\ &\\ &\int_0^{2\pi}sen^2t·cost\;dt=\\ &\\ &2\pi^2+3\pi^2+\left.\frac{sen^3t}{3}\right|_0^{2\pi}= 5\pi^2\approx 49.34802201\end{align}$$

Aunque no es la misma figura veamos si se parece al elipsoide de semiejes pi, 2, 2

V=(4/3)pi·pi·2·2 = (16/3)pi^2 = 52.63789.

Si, no es lo mismo pero se parece, la elipse es algo más grande que la cicloide, luego es buena señal de que está bien hecho.

Y eso es todo.

¡Gracias! Profesor por su gran ayuda y si alguna falta le he cometido a sido sin ninguna mala intención. 

Puedes cambiar la puntuación de la pregunta de esa serie y así seguiré contestando.

Y ahora una mala noticia. Leí mal esta pregunta y calculé el volumen en lugar del área. No se si el área será más fácil o más complicada todavía, aunque me parece que similar. El caso es que me costó lo suyo responder esta pregunta porque esa fórmula que he usado no salía en ningún sitio. Te pediría por favor que volvieses a mandar la pregunta para esta vez contestar de verdad a lo del área.

Y si me pudieras decir el libro me vendría bien para ver si ahí os salen las fórmulas de área y volumen en paramétricas o hay que deducirlas, cambia mucho el trabajo de una forma u otra.

Muchos saludos.

¡Gracias! Profesor la respuesta del Volumen tiene ciertos detalles que son interesante, el hecho que un matemático no se hecha para atrás ni arruga el entrecejo. MUCHAS GRACIAS, estoy aprendiendo 

Ya corregí Profesor, pero aun estoy revisando la respuesta tiene cierto de interés.