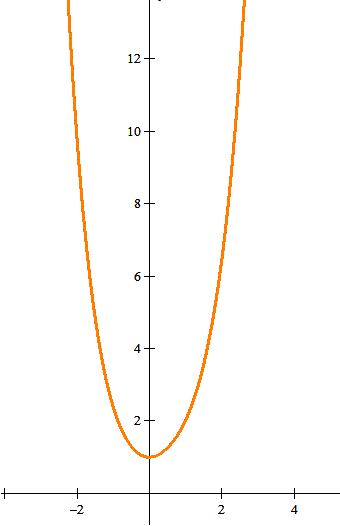Hola! ¿Podrías ayudarme con esta ecuación diferencial?

Juan Villega!

a)

Primero se calcula la solución general de la ecuación homogénea

y'' - y = 0

su ecuación característica es

k^2 - 1 = 0

luego las raíces son k=1 y k=-1

La solución general de la homogénea es

ygh = C1·e^(x) + C2·e^(-x)

Ahora se debe calcular una solución particular de la completa. Cuando la función de la derecha es un polinomio se prueba con un polinomio genérico del mismo grado, con todos los tñerminos desde 0 hasta el grado

p(x) = ax^2 + bx + c

p'(x) = 2ax + b

p''(x) = 2a

sustituimos estos valores en la ecuación diferencial

2a - ax^2 - bx - c = x^2 - x + 1

igualando los términos del mismo grado

-a = 1   ==>  a =-1

-b = -1  ==>  b = 1

2a-c = 1  ==>  -2-c = 1  ==> c = -3

Luego el polinomio solución particular de la completa es

ypc =  -x^2 + x - 3

Y finalmente sumando la general de la homogénea con la particular de la completa tenemos la generalde la completa, que llamaremos simplemente y

y = C1·e^x + C2·e^(-x) -x^2 + x - 3

------------------------

b)

Para y(0)=1 tenemos esta ecuación

C1·e^0 + C2·e^(-0) - 0^2 + 0 - 3 = 1

1)  C1 + C2 = 4

Y para y'(0)=0 primero derivamos y y luego sustituimos x por 0. Aunque se puede hacer todo en un paso

y' = C1·e^x  - C2·e^(-x) - 2x +1

2)  C1 - C2 + 1 = 0

tenemos las ecuaciones 1 y 2, vamos a sumarlas tal como están

2C1 + 1 = 4

2C1 = 3

C1 = 3/2

C2 = 4-C1 = 4-3/2 = 5/2

Luego la solución con esas condiciones iniciales es

y=(3/2)e^x + (5/2) e^(x) - x^2 + x - 3

c) Y la gráfica es:

Y eso es todo.