Anónimo
Demostracion de algebra lineal( detrminantes e inversas)
Hola! De la manera más atenta y humilde solicito ayuda para resolver esta demostración, un cordial saludo y gracias!
Suponga que la matriz A de nxn no es invertible. Muestre que (A) (adjA) es la matriz cero
1 Respuesta
·
Si la matriz no es invertible entonces su determinante es 0.
Hay una propiedad que puedes ver en la wikipedia que dice
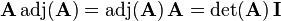para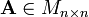 
.
http://es.wikipedia.org/wiki/Matriz_de_adjuntos#Propiedades
Luego si el determinante es 0 el producto es 0 por la matriz identidad y eso es la matriz nula.
El demostrar esa propiedad no es muy difícil, pero es complicadísimo de explicar aquí se necesitaría una pizarra. Se basa en que el determinante se puede calcular por el desarrollo por una fila o columna. Entonces si dibujas una matriz y su adjunta al lado y haces el producto verás que los elementos c_ii de la diagonal principal de la matriz producto C son el desarrollo por la fila i-esima del determinante. Y que los elementos c_ij de fuera de la diagonal principal corresponden al determinante de una matriz cuyas filas i y j iguales, luego su determinante es 0 y fuera de la diagonal serán todo ceros. Como en este caso el determinante es 0 la diagonal principal también tendrá ceros y será la matriz nula.
·
Y eso es todo.