¿Como debo calcular los limites de esta función Realiza la gráfica de la siguiente función, indique por dónde atraviesa el eje d

·

Esta es la gráfica:

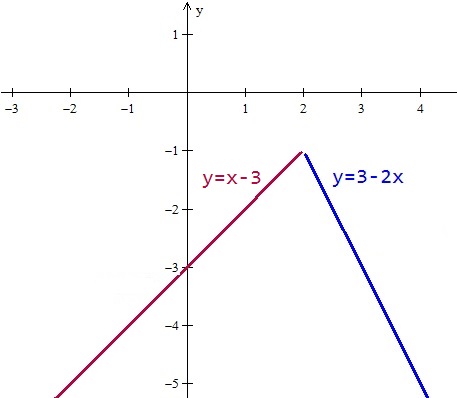
El eje Y se atraviesa cuando x=0, luego la función que debe emplearse es la roja

y = x-3 = 0-3 = -3

Luego el punto es el (0, -3)

·

Los límites en x=2 por la izquierda y derecha son:

$$\begin{align}&\lim_{x\to 2_-}f(x)=\lim_{x \to 2}(x-3)=2-3=-1\\&\\&\lim_{x\to2_+}f(x) = \lim_{x\to 2}(3-2x)=3-2·2=-1\end{align}$$

Como son iguales hay límite y su valor es -1

La función en x=2 no existe, luego carece de sentido la pregunta de si es continua.

Si existiese y su valor fuera -1 entonces sería continua ya que coincidiria su valor con el límite. Pero tal como se ha definido la respuesta es que no existe la función en x=2.

------------------------

a) En t=2 es continua, tanto por la izquierda como por la derecha tenemos la misma función que es una sencilla función lineal f(t)=-100t+600 continua de toda la vida.

·

b) En t=5 deberemos comprbar si coinciden los límites

$$\begin{align}&\lim_{t\to 5_-}f(t) = \lim_{t \to 5}(-100t+600) =\\&-100·5 + 600 = 100\\&\\&\\&\lim_{t\to 5_+}f(t)= \lim_{t\to5 }(-100t+110)=\\&-100·5+110 = -390\end{align}$$

No coinciden los límites laterales, luego la función no es continua en t=5

c) En t=15 tenemos el extremo derecho de la función y no hay límite por la derecha, será continua solo con que el valor de la función coincida con el límite por la izquierda.

Y el límite por la izquierda es el valor de la función en 15, luego es continua.