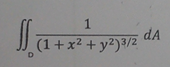Como podría emplear un cambio de variable a este ejercicio
Donde {(x,y) 0=<x=<1 y 0=<y=<x}
Empleando para ello un cambio de variable.
1 respuesta
Diosa Lara!
·
Las integrales con raíces cuadradas son de lo más ingrato ciertamente.
Parece todo predispuesto para un cambio a coordenadas polares pero no es tan sencillo porque el dominio no es un sector circular es un triángulo con vértices
(0,0), (1,1), (1,0)
El típico triángulo rectángulo con el vértice en (0,0), la base de longitud 1 en el eje X positivo y el ángulo de 45º en el origen.
Está claro que en polares el ángulo theta valdrá entre 0 y pi/4
Y el radio-vector valdrá entre 0 y algo más complicado de calcular. Ese algo será
$$\begin{align}&\rho=\sqrt{1+y(\theta)^2}\end{align}$$Si conoces la representación gráfica de la tangente sabes que es la altura del ángulo medida sobre la recta x=1, luego el límite suoperior de rho es
$$\begin{align}&\sqrt{1+tg^2\theta}=\sqrt{sec^2\theta}= \frac 1{\cos\theta}\end{align}$$Y por otra parte hay que multiplicar la integral por el jacobiano de l cambio de variable a polares.
$$\begin{align}&x=\rho·\cos\theta\\&y=\rho·sen\theta\\&\\&\frac {dx}{d\rho}=\cos\theta\quad\quad \frac{dx}{d\theta}=-\rho\, sen\,\theta\\&\\&\frac {dy}{d\rho}=sen\theta\quad\quad \frac{dy}{d\theta}=\rho\, \cos\,\theta\\&\\&\text{y el jacobiano es}\\&\\&I=\rho\, \cos^2\theta+\rho\, sen^2\theta=\rho\\&\\&\text{con todo esto queda la integral}\\&\\&\int_0^{\pi/2}\int_0^{1/\cos\theta}\frac{\rho}{(1+\rho^2)^{3/2}}d\rho\;d\theta\\&\\&\end{align}$$Al menos la integral interna la veo fácil con el cambio
t = 1 + (rho)^2
Te dejo que continúes y si no puedes terminar me lo dices.
entendí una parte hasta que llego a los cambios
ρ=√1+y(θ)^2
:(
El radio vector rho máximo en cada ángulo es la distancia entre el origen(0,0) y el cateto opuesto de ese triángulo rectángulo que es la recta x=1.
Ese radio vector por lo tanto es
sqrt(1^2+y^2)
Donde y es una altura que varía entre 0 y 1 dependiendo del ángulo, por eso puse [y(theta)]^2 o como no me gusta el exceso de paréntesis escribo y(theta)^2 que para mí y el programa Máxima es lo mismo, de ahí lo aprendí.
Entonces por suerte esa altura sobre la recta y=1 coincide con el valor de la tangente del ángulo theta. De ahí se sigue que el radio vector mide
sqrt[1+tg^2(theta)]
que si no lo sabes es facil comprobar que es lo mismo que
sqrt[sec^2(theta)] = sec(theta) = 1/ cos(theta).
Y luego supongo que sabrás o tendrás en la teoría como se calculan los jacobianos. No lo he puesto con los determinantes porque el editor funciona mal con matrices y determinantes.
