¿Cuál es la respuesta a estos ejercicios?

·

Cada ejercicio debe ir en una pregunta. En esta haré el primero, los otros tendrás que mandarlos en tantas preguntas como ejercicios quieras que resolvamos.

Y la resolución y entendibilidad de la foto está en el límite, si pudieras escribirlos a mano también sería el complemento perfecto.

Yo creo que en segundo trozo de la función falta algo, pone

-2+11    Si x>4

Y no suele darse la suma de dos constantes como definición, sin duda falta alguna x ahí.

Gracias, Disculpe mi cámara es un poco complicada en cuanto a esto de los mp, Anexo información del contenido de los ejercicios.

1) Dada la siguiente función determina el dominio, Rango y Grafique

F(x) { X2-4x+3 Si -1 Menor o igual(<-) X < 4

        { -2+11 Si X > 4

        { 6 SI X=4

2) Sea f(x) = x2-1, h(x) = Raiz cuadrada de x+1

J(X) = Valor absoluto de x-1/2   Calcular limite cuando tiende a 2, [J(X)/H(X)] elevado a f(x)

3) aplique la definicion formal del limite 

limite cuando tiende a x>a    X2+X+A-A2/X+A = -2A+1

4) Encuentre aplicando las propiedades limite cuando tiende a x>8 

x2/3 + 3 raizcuadrada de x / 4-10/x

5) calcule limite cuando tiende a 5 pi/4     2-2 ctg X / cosx  - sen x

6) Limite cuando por tiende a 2-3h raíz cuadrada sobre 3, x3-6x2+12x-8

7) Limite cuando tiende a +infinito (raizcuadrada de por (x-a) - x) todo esto dentro de la raíz

x2 lo coloque así y a2 es x elevado al 2 y a elevado al 2 en el ejercicio 3

Y en el 2 ejercicio j(x) es un valor absoluto con fracción y calcular también el limite es un corchete con una fracción elevada a f(x) de j(x) y hy(x)

PD: pido ayuda porque en clases solo vi definición de rango función, limite tipos de funciones pero al colocar valor absoluto no entendía por motivos de desconocer y de iual forma trabajar con el numero pi en el limite y el limite elevado a 2/3 Gracias si por esta vía puedo encontrar alguna respuesta a estas dudas

Pero yo sigo pensando lo mismo, en la línea

-2+11    Si x>4

Falta una x o dos elevadas a lo que sea por fuerza, porque eso tal como está nunca se escribiría, te lo aseguro, que pueda ser

-2x + 11

- 2 + 11x

-2x^3 + 11x^2

Eso es lo que yo no se, aunque me inclinaría por -2x+11.

Los enunciados de los ejercicios 2 en adelante guárdalos porque tendrás que ponerlos en otras preguntas, una por cada ejercicio.

¿Entonces dime qué hago? Yo pondría -2x+11 en el ejercicio primero cuando X > 4

Es correcto, seria completando -2x+11 verificando el ejercicio le faltaba el por al 2 que es 2x

Ahora si, ya puede hacerse.

El dominio es Dom f = (-1, +infinito)

El rango es un tanto raro de calcular por tener dos o tres trozos, veamos cual es el rango de cada uno. Supongo que ya habréis dado derivadas, máximos y mínimos

f(x)=x^2-4x+3

Es una parábola en forma de U luego tendrá un mínimo, vamos a calcularlo derivando e igualando a 0

f'(x) = 2x -4 =0

2x=4

x=2

luego el mínimo está en x=2 y es

f(2)= 2^2-4·2+3 = 4-8+3 = -1

y el máximo está en x=-1 ya que está más alejado del vértice x=2  que el otro extremo del intervalo x=4

Luego el máximo es

f(-1) = (-1)^2-4(-1)+3 = 1+4+3=8

Luego el rango de la primera función es [-1, 8]

·

Y la función -2x+11 es una recta de decrece, luego su máximo estará al principio y decrecerá hasta -infinito, su rango será

(-infinito , 3)

el 3 no entra porque en x=4 no esta definida con esa función

Finalmente el punto y=6 también entre en el rango, pero como ya estaba en el intervalo [-1, 8] no añade nada

Rango f = (-infinito, 3) U [6] U [-1, 8]

Rango f = (-infinito, 8)

Y la gráfica es esta:

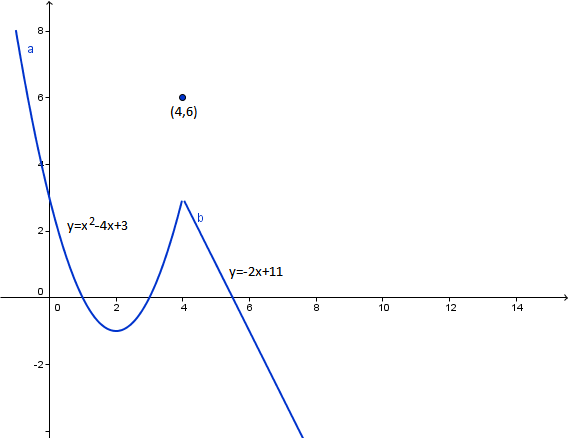
Y eso es todo, espero que te sirva y lo hayas entendido. Como te decía manda los ejercicios que quieras pero de uno en uno. Y antes no olvides puntuar esta pregunta.

Gracias sr 
Valero Angel Serrano Mercadal por su oportuna ayuda, y para este ejercicio.

Sea g(x) = 3x+1/x-2 

J(x) = valor absoluto x-1/2

Calcular limite cuando tiende a 4 [g(x).j(x)]

Gracias