¿Cómo encontrar la inversa de una función?
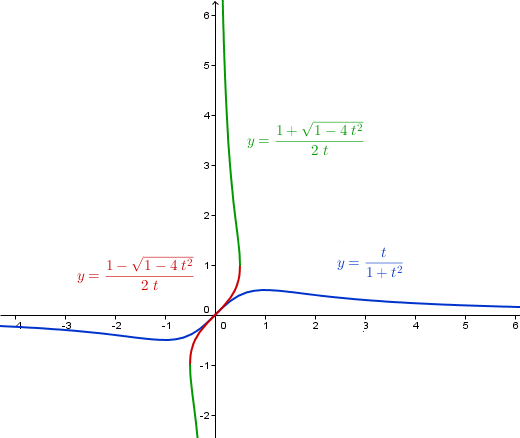
Se que para encontrar la inversa de una función, f(x) = y, se debe despejar x. Pero no puedo despejar x de la expresión y = x/(1+x^2)
Es decir, que no puedo encontrar la regla de correspondencia de la inversa de f(x) = x/(1+x^2).
Y sí tiene inversa, porque la función es inyectiva.
¿Cómo le hago?
1 Respuesta
·
Si se puede despejar x, luego se estudia el dominio para que sea una función.
$$\begin{align}&y = \frac {x}{1+x^2}\\&\\&y +yx^2=x\\&\\&yx^2-x+y=0\\&\\&\text{esto es una ecuación de segundo grado en x}\\&\\&x=\frac{1\pm \sqrt{1-4y^2}}{2y}\\&\\&\text{luego hay dos funciones inversas}\\&\\&f_1^{-1}(x)=\frac{1-\sqrt{1-4x^2}}{2x}\\&\\&f_2^{-1}(x)=\frac{1+ \sqrt{1-4x^2}}{2x}\end{align}$$Son funciones algo complicadas, lo mejor será hacer la gráfica.
La azul es la función normal y la roja y verde son las inversas que son un tanto raras.
La roja es la inversa cuando f está definida en el intervalo entre el mínimo y el máximo de f
La verde es la inversa cuando la función f está definida en el dominio (-infinito, mínimo) U (máximo, infinito)
Incluso si quisieras podrías subdividir en dos funciones la verde.
El máximo y mínimo supongo que lo sabrás calcular mediante derivadas. Si no es así me lo dices.
¡Gracias!
Es cierto, porque la función realmente no es inyectiva. Sólo es inyectiva en algunos subintervalos (donde la función es creciente y donde es decreciente) y por eso se obtienen dos inversas.
Y no se me había ocurrido emplear la fórmula del "chicharronero" para despejar x.
Muchas gracias!!!
Gracias por todo el apoyo, hasta pronto - marita reveles morado