Determine la inversa de la siguiente función y grafique ambas en el mismo plano cartesiano. F(x)= 3/2x+3
Necesito Determinar la inversa de la siguiente función y graficar ambas en el mismo plano cartesiano.
f(x)= 3/2x+3
Son funciones inversas
Necesitaría me ayuden en este tipo de función
Si así es, gracias por la corrección
Me ayudas?
La función es una recta y la inversa va a ser otra recta simétrica respecto de la recta y=x
Para hallar la inversa de una función lo primero hay que despejar la x
partiendo de y=f(x) quedará
x=f^-1(y)
y para que quede como una función de x, se intercambiaran los papeles de x y y.
y=f^-1(x)
$$\begin{align}&y=F(x)\\&\\&y=\frac{3}{2}x+3\\&\\&y-3= \frac 32 x\\&\\&\frac 32x= y-3\\&\\&x=\frac 23(y-3)\\&\\&x=\frac 23y -2\\&\\&\text{ahora cambiamos los papeles}\\&\\&y =\frac 23x-2\\&\\&\text{o prodríamos haber puesto directamente}\\&\\&F^{-1}(x) = \frac 23x-2\\&\end{align}$$Y siendo dos rectas no hay ningún problema para dibujarlas, calculas dos puntos de cada una
Para F(x) = (3/2)x +3
Cuando x=0 ==> F(0) = 3 ==> (0, 3)
Cuando x=2 ==> F(2) = 3+3= 6 ==> (2, 6)
Para F^-1(x) = (2/3)x-2
x=0 ==> F^-1(0) = -2 ==>(0,-2)
x=3 ==> F^-1(3) = 2-2 = 0 ==>(3, 0)
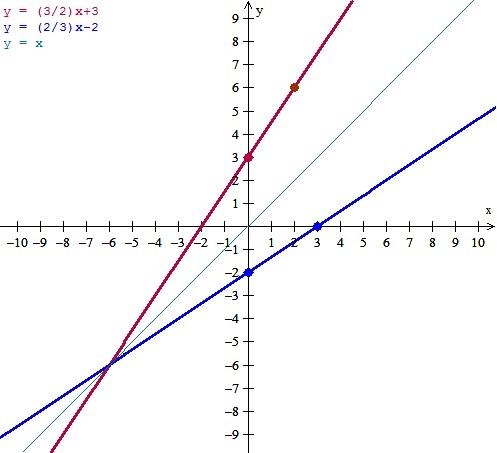
La simetria respecto de la recta verde es señal de que está bien.
·
Y eso es todo.
Ok, de acuerdo gracias, solo para finalizar me revisas este ejercicio, por favor:
Determine (f⁰g) dadas las funciones siguientes.
f(x)= 2x^2-9x-5
g(x)=3x-4
(fog)(x)= 2(3x-4)^2 - 9(3x-4) - 5
= 2(9x^2-8) - 27x + 36 - 5
= 18x^2 - 16 - 27x + 39
= 18x^2 - 27x - 23
ya verifique esta mala, me falto en el primer termino multiplicar el primero por el segundo al cuadrado
$$\begin{align}&f(x)= 2x^2-9x-5\\&\\&g(x)=3x-4\\&\\&(fog)(x)= 2(3x-4)^2 - 9(3x-4) - 5\\&\\& = 2(9x^2-24x+16) - 27x + 36 - 5\\&\\&= 18x^2-48x+32 -27x+31\\&\\& = 18x^2 - 75x + 63\end{align}$$El cuadrado del binomio lo tenías bastante mal hecho.
