Apoyo con ejercicio de 1era. Derivada,valores máx,mínimos,puntos de inflexion,intervalos de crec.,decrecimiento. Y concavidad

·

Haremos la primera derivada y la igualaremos a 0 para hallar los puntos críticos. Y la segunda igualada a 0 para hallar los puntos de inflexión.

$$\begin{align}&y=(x^2-x-1)^2\\&\\&y'=2(x^2-x-1)(2x-1)\\&\\&\\&\\&y''= 2\left((2x-1)(2x-1)+2(x^2-x-1)  \right)=\\&\\&2(2x-1)^2+4(x^2-x-1)=\\&\\&8x^2-8x +2+4x^2-4x-4 \\&\\&y''=12x^2-12x-2\\&\\&\text{Los puntos críticos son los que }f'(x)=0\\&\\&2x-1=0\implies2x=1\implies\\&x_1=\frac 12\\&\\&x^2-x-1=0\implies x=\frac{1\pm \sqrt{1+4}}{2}\implies\\&x_2=\frac{1-\sqrt 5}{2}\approx -0.618034\\&x_3=\frac{1+\sqrt 5}{2}\approx 1.618034\\&\\&\text {veamos si son máximos o mínimos con }f''(x)\\&\\&f''\left(\frac 12\right)=-5\lt0\implies \text{máximo}\\&f''(-0.618034)=10\gt0\implies \text {mínimo}\\&f''(1.618034)= 10\gt 0\implies \text{mínimo}\\&\\&f(x_2)\; y\; f(x_3)=0 \text{ por ser raíces de }x^2-x-1\\&f(0.5)=1.5625\\&\\&\text{Máximo =}(0.5,\;1.5625)\\&\text{Mínimos=} \{( -0.618034,0), \quad(1.618034,0)\}\\&\\&\text{Puntos de inflexión cuando }f''(x)=0\\&\\&12x^2-12x-2=0\\&\\&x=\frac{12\pm \sqrt{144+96}}{24}=\frac{3\pm \sqrt{15}}{6}\\&\\&x_{i_1}\approx -0.145497\\&x_{i_2}\approx 1.145497\\&\\&f(-0.145497) =f(1.145497)=0.694445\\&\\&\text{Puntos de Inflexión:}\\&(-0.145497,\;0.694445)\\&(1.145497,\;0.694445)\\&\\&\end{align}$$

Salgamos del editor de ecuaciones que en él no se pueden escribir reflexiones profundas.  Ya hemos calculado los mínimos, máximos y puntos de inflexión.

Ahora los intervalos de crecimiento o decrecimiento se pueden calculan mediante el signo de la derivada primera, esto se puede hacer evaluando puntos entre las raíces de esa derivada, o conociendo cómo se comporta la derivada. Y tambíen se pueden calcular sabiendo que donde hay un mínimo antes es decreciente y luego creciente y donde hay un máximo antes crece y después decrece.

Usaré este último. Como en x= -0.618034 hay mínimo antes decrece y luego crece hasta el maximo en x=0.5 y luego decrece hasta 1.618034 donde hay un mínimo y después crece hasta infinito.

Y para la concavidad se calcula el signo de la derivada segunda, aquí usaré que

f ''(x) = 12x^2 - 12x-2

Es un polinomio de grado 2 con signo positivo en x^2, luego es positiva a la izquierda y derecha de las raíces y negativa entre ellas. Cuando sea positiva diré que la función es cóncava hacia arriba y cuando sea negativa es cóncava hacia abajo. Es inútil intentar entenderse con las palabras cóncava y convexa, cada país, cada libro, cada autor dice una cosa distinta sobre lo que es una cosa y otra.

Cóncava hacia arriba es en forma de U y cóncava hacia abajo en forma de iglú.

Pues con todo este rollo queda que los intervalos son:

Y finalmente nada mejor que una gráfica:

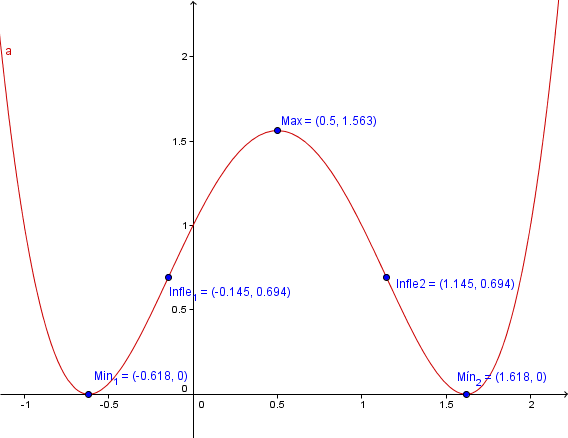
Y eso es todo.