·
Pues este es un problema bien claro de integrales múltiples con cambio de coordenadas a cilíndricas.
La superficie x^2+y^2+z^2=a^2 es una esfera centrada en el origen de radio a
La superficie x^2+y^2=ax es un cilindro vertical.
x^2 - ax + y^2 =0
(x- a/2)^2 -(a/2)^2 + y^2= 0
(x- a/2)^2 + y^2 = (a/2)^2
Luego es un cilindro con centro
(a/2, 0)
y radio a/2.
Es como un tubo de aspirinas metido en la parte derecha de una naranja.
Calculemos cuanto mide su área para cada plano z=c
La intersección del plano con la esfera será una circunferencia
x^2+y^2+c^2=a^2 ==>
x^2+y^2 = a^2-c^2
La intersección con la curva
x^2+y^2=ax
es
ax =a^2-c^2
x = a - (c^2/a)
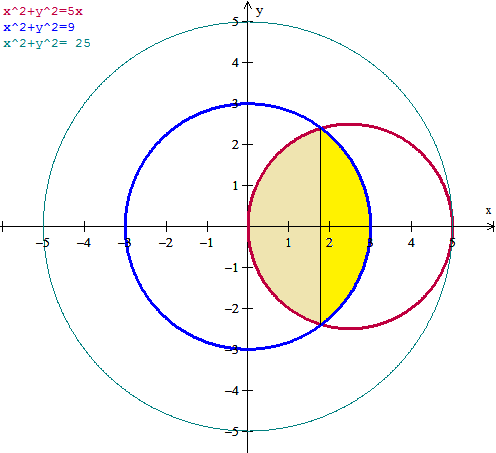
En este ejemplo a=5, c=4.
x^2+y^2=5^2-4^2 = 3^2
Es la circunferencia azul de radio 3 y el área en el plano z=c es la coloreada que se divide en dos zonas por la recta
x=5- (4^2/5) = 5- 16/5 = 9/5=1.8
y el área calculada con integrales es
$$\begin{align}&A=2\left(\int_0^{a-\frac{c^2}a}\sqrt{ax-x^2}dx+\int_{a-\frac{c^2}{a}}^{a^2-c^2}\sqrt{x^2-(a^2-c^2)} \right)=\\&\\&\text{y esto es laborioso de integrar, la verdad}\end{align}$$Y el resultado que he podido obtener con el programa máxima es una expresión completamente inmanejable. Y ese resuldo habria que integrarlo con respecto a c entre -a y a. Intentar demostrarlo sin integrales dobles y cambio múltiple de variable parece que es algo descabellado e inviable,al menos tal como lo he intentado.
·
Aquí ya trabajé mucho. Si me mandas otra pregunta intento a ver si tomando áreas de corte verticales con planos x=c se puede hacer algo.

