Hallar el área de la región limitada por la parábola ycuadrada=4x y la recta y=2x-4

·

Hagamos primero la gráfica para que sea más fácil deducir la integral.

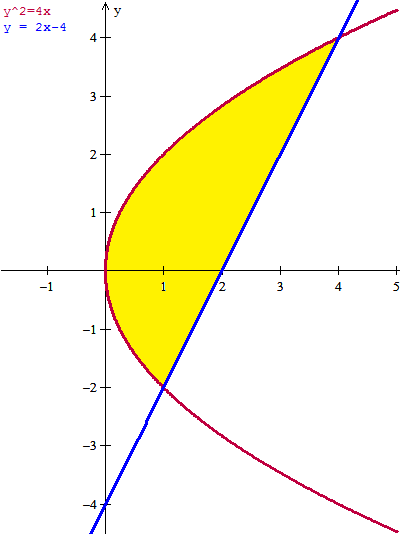
Como puedes ver si integramos respecto de x tendrámos que hacer dos integrales porque entre 0 y 1 es área entre función roja y función roja y entre 1 y 4 entre función roja y azul.

Mientras que si integramos respoecto de y tenemos que entre -2 y 4 es función azul menos roja y se calcula el área con una sola integral. Aunque los tenemos a la vista vamos a calcular la coordenada y de los los cortes

y^2=4x

y=2x-4  ==> -2y = -4x +8

Y sumándolas

y^2-2y = 4x-4x+8

y^2 - 2y - 8 = 0

que se factoriza a la vista

(y +2)(y-4) = 0

Luego los cortes son

y=-2

y=4

Como vamos a integrar respecto de y las funciones deben estar expresadas de la forma

x=f(y)

La azul que sera la superior es

y=2x-4

2x=y+4

x = y/2 + 2

Y la roja que es la inferior es

y^2=4x

x = y^2/4

Y el área será:

$$\begin{align}&A=\int_{-2}^4 \left(\frac y2+2- \frac {y^2}{4}\right)dy=\\&\\&\left[\frac{y^2}{4}+2y-\frac {y^3}{12}  \right]_{-2}^4=\\&\\&4+8-\frac{64}{12}-1+4-\frac{8}{12}=\\&\\&15-\frac{72}{12}=15-6=9\end{align}$$

Y eso es todo.

¡Gracias! Una consulta, cuando se empiezan a calcular las coordenadas sale y^2=4x y luego y=2x-4 ==> -2y = -4x +8, la pregunta es de dónde sale el 8? Le  agradeceria mucho por su ayuda.