Como puedo calcular el valor exacto de la integral

Hacemos el dibujo del dominio de integración, así lo tendremos claro.

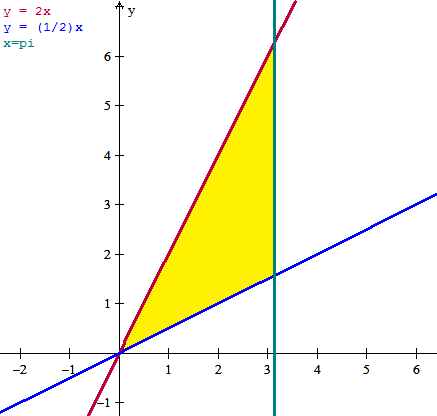
Es la región pintada de amarillo. Vemos que en el eje x la figura comienza en x=0 y termina en x=pi, luego podemos tomar 0 y pi como límites de integración en x.

Y en el eje Y la figura está comprendida entre la recta azul y=(1/2)x y la recta roja y=2x

Luego esos dos son los límites de integración en y.

Y tenemos que integrar la función senx en ese dominio. Luego está el dA, diferencial de área, que es el diferencial de y por el diferencial de x.

$$\begin{align}&\iint_Rsen \,x\;dA=\\&\\&\int_0^{\pi}\int_{x/2}^{2x}sen\,x\;dy\,dx=\\&\\&\text{primero se integra respecto de y}\\&\text{luego senx es una constante}\\&\\&=\int_0^\pi senx·y|_{x/2}^{2x}dx=\\&\\&\int_0^\pi senx·\left(2x-\frac x2\right)dx=\\&\\&\frac 32\int_0^\pi x\,sen\,x\,dx=\\&\\&\text{se resuelva por partes}\\&\\&u=x\quad\quad\quad\quad du=dx\\&dv=sen\,x\,dx\quad v=-cosx\\&\\&=\frac 32\left(-x \cos x|_0^\pi+\int_0^\pi \cos x \;dx\right)\\&\\&\frac 32\left(-\pi(-1)+0·1-sen\,x|_0^\pi\right)=\\&\\&\frac 32(\pi+0-0+0)=\frac{3\pi}2\end{align}$$

·

Y eso es todo.