Resolver ejercicio de grafos y arboles algoritmos U5
Dada la siguiente gráfica
Anexo la correspondiente gráfica para la actividad 6 de la unidad 5 plan de trabajo para aplicar el algoritmo de Warshall
Encuentra la matriz de pesos mínimos, usando el algoritmo de Warshall. Muestra los pasos del algoritmo.
1 Respuesta
·
Esto sin pizarra se explica muy mal.
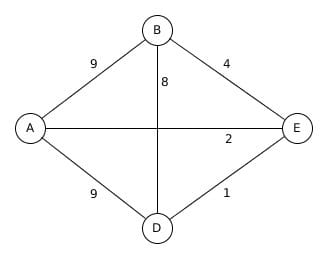
Formamos la matriz de las distancias
A B D E
A - 9 9 2
B 9 - 8 4
D 9 8 - 1
E 2 4 1 -
Primer paso
Veremos si se mejora la distancia pasando por el el punto A. Se tomarán todos las distancias XY con X y Y distintos de A
Como las distancias son simétricas, solo tomaremos los pares XY donde X<Y. Si hay mejora en XY se hace esa misma mejora en YX
Por ejemplo para la distancia BD, queremos saber si es peor que la suma de distancias BA+AD para ello tomamos en la fila B la columna A que es 9 y en la fila A la columna D que es 9 también y los sumamos y comparamos con el elemento BD
BD --> 9+9 = 18 > 8 permanece el 8
Para ver si BA+AE < BE tomaremos BA=9 y AE=2 sumamos y comparamos con BE=4
BE --> 9+2 = 11 > 4 permanece el 4
DE --> 9+2 = 11 > 1 permanece el 1
·
Segundo paso.
Veremos si se mejora la distancia pasando por el punto B, luego dado el recorrido XY veremos si XB + BY es más corto. Ahora se tomarán diostancias de pares XY donde ninguno de los dos es la B
AD --> 8+9 = 17 > 9 permanece el 9
AE --> 9+4 = 13 > 2 permance el 2
DE --> 8+4 = 12 >1 permanece el 1
·
Tercer paso.
Hacemos lo mismo con la D, que vaya lio han creado por no poner la letra C.
Luego compararemos XD+DY con XY
AB ---> 9+8 = 17 > 9 permanece el 9
AE ---> 9+1 = 10 > 2 permanece el 2
BE ---> 8+1 = 9 > 4 permanece el 4
·
Y el cuarto y último paso es pivotando sodr el elemento E, se comparan XE+EY con XY
AB ---> 2+4 = 6 < 9 Luego se adopta AB=BA=6 y las trayectorias más cortas son
AB=AE+EB; BA=BE+EA
AD ---> 2+1 = 3 < 9 Luego se adopta AD=DA=3 y las trayectorias más cortas son
AD=AE+ED; DA=DE+EA
BD ---> 4+1 =5 < 8 Luego adoptamos BD=DB=5 y la trayectoria a seguir será
BD= BE+ED; DB=DE+DB
La matriz que queda al final es
A B D E
A - 6 3 2
B 6 - 5 4
D 3 5 - 1
E 2 4 1 -
·
Y eso es todo.
