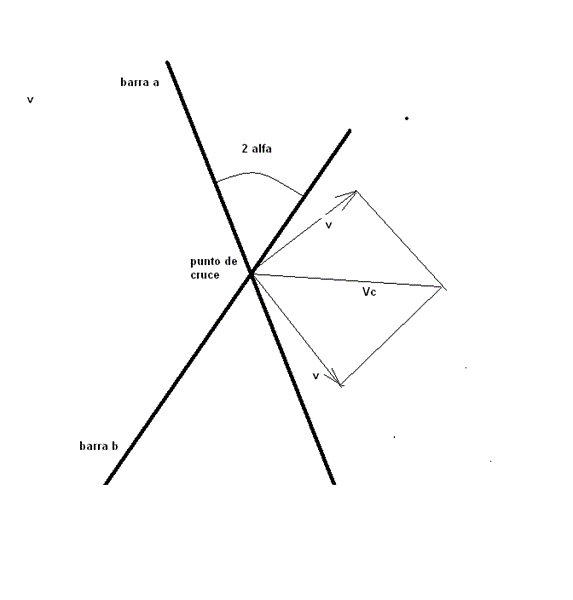
Dos barras se cruzan bajo el ángulo 2α. Cual será la velocidad
Dos barras se cruzan bajo el ángulo 2α y se mueven con igual velocidad v y perpendicularmente así mismas.
¿Cuál será la velocidad del punto de cruce de las barras?.
El grafico muestra como es el sistema a analizar. Como se muestra en el grafico siguiente.
En este ejercicio tengo dudas, ya que el libro da un resultado, pero yo encontre otro resultado por eso quiero que me ayuden, por favor

Respuesta de albert buscapolos Ing°
1