Resolver los siguiente ejercicios de funciones inversas unidad 6

1) Obtén la función inversa de las siguientes expresiones:

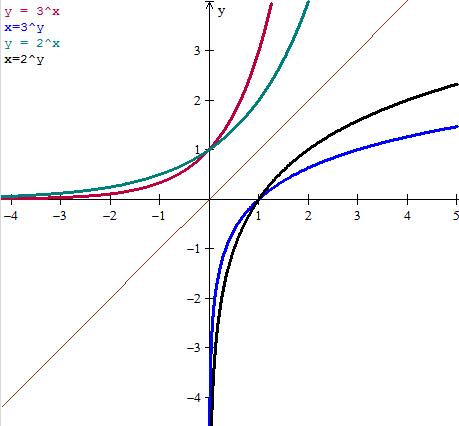
  1. a) f(x) = 3^x , X = conjunto de los números reales
  2. b) f(x) = log2x , X = conjunto de los números reales positivos

2) Grafica las funciones y sus funciones inversas

3) Di si las funciones son uno a uno y por qué

1 respuesta

Respuesta
1

·

1)

$$\begin{align}&f(x)=3^x\\&f^{-1}(x) = log_3x\quad \\&\\&Dom f^{-1}= \mathbb R^+\\&\\&\\&f(x)=log_2x\\&f^{-1}(x)=2^x\\&\\&Domf^{-1}=\mathbb R\end{align}$$

2)

Las funciones logarítmicas no neperianas no suelen estar en el repertorio de los programas de hacer gráficas. Para poder graficarlas habrá que hacer un cambio de base o poner las exponenciales de forma implícita con las variables cambiadas, por ejemplo

x=3^y      para la inversa de y=log_3(x)

x=2^y      para la inversa de y=log_2(x)

3)

Son todas funciones uno a uno (inyectivas) se puede demostrar analíticamente, pero seguramente te han hecho hacer las gráficas para que veas que son monótonas (crecientes en este caso) y eso hace que sean inyectivas.

Y eso es todo.

Añade tu respuesta

Haz clic para o

Más respuestas relacionadas

Función exponencial Y=entre parentesis 1/3 elevado a la x-2 y mas abajito +5.

Necesito esta repuesta, también me piden si es inyectiva, sobreyectiva biyectiva... Así como también la gráfica, Hallar :dominio, rango y los corte, con y con y con x
2 respuestas

¿Valor absoluto es inyectiva esta función?

Si yo tengo la funcoin f(x)=|x^3 - 1| si miro el gráfico a ojo digo que NO es inyectiva porque si trazo una recta me coincidirán dos puntos... El problema es que analíticamente me da que SI es inyectiva ya que si tomo valores como 1, -1 2 -2 3 -3 4...
1 respuesta

¿Cómo encontrar la inversa de una función?

Se que para encontrar la inversa de una función, f(x) = y, se debe despejar x. Pero no puedo despejar x de la expresión y = x/(1+x^2) Es decir, que no puedo encontrar la regla de correspondencia de la inversa de f(x) = x/(1+x^2). Y sí tiene inversa,...
1 respuesta

Dudas con composición de funciones matemáticas

Valero ASM! Por lo visto entonces tu profesión es matemático puro. ¿Dónde te preparaste en una universidad, instituto o en otro lugar? ¿Cómo son los centros de estudios allá en España?, Te mando mis dudas: Primera parte: Si f y g son ambas funciones...
1 respuesta

Demuestre que la funcion f: [-2,2]→[8,16] definida por f(x)=3x^2+2x ,es

A) Creciente. Si no es, indicar intervalo de crecimiento y de decrecimiento. B) Uno a uno . Si no es, acote el dominio de la función. C) Determinar su inversa (1 punto). No entiendo esta parte de matemática
1 respuesta

Ejercicios de gráficas y funciones

1. Traza la gráfica de la siguiente función exponencial f(x) = 4x 2. Traza la gráfica de la siguiente función y escribe sus características propias f(x) = sen x 3. Cual es el periodo de la siguiente función f(x) = sen 6x
1 respuesta

Despeje con logaritmos natural

Despejar 'y' de:
1 respuesta

Demostrar que la función tan(x)

Considerando la función demuestre que: a). Tanh^-1x existe en x que pertenece a (-1,1) b) tanh^-1x = 1/2 ln [ (1+x) / (1-x)] c) d/dx [tanh^-1x] = 1 / (1-x^2)
1 respuesta

Demostración de Función Hiperbólica

Considerando la función tanh(x) demuestre que: tanh^-1(x) existe en x E (-1,1)
1 respuesta

Calcular función exponencial:

De la siguiente función exponencial: la x es elevado Determine: a) El dominio máximo de la función (IR, IR+ ó IR-) b) El ámbito de la función (IR, IR+ ó IR-) c) El punto de intersección con el eje y d) La función es creciente o decreciente.
1 respuesta