Hallar la ecuación tangente a la elipse
Dentro de la Geometría Analítica
Hallar la ecuación tangente a la elipse
$$\begin{align}&x^2/10+(2y)^2/5=1\end{align}$$que son paralelas a la tangente 3x+2y +7=0.
1 respuesta
·
Imagino que querrás decir:
que son paralelas a la "recta" 3x+2y +7=0
Ya que dicha recta no es tangente a la elipse.
Esto tendría dos formas de solución, una más propia del Álgebra mediante el cálculo de rectas que solo intersecan a la elipse en un solo punto. Y otra más de Cálculo mediante la fórmula de rectas tangentes en un punto cuya pendiente es la derivada.
¿Cuál habría que usar?
$$\begin{align}& \end{align}$$¡Bueno, vamos con ello!
Por ser una recta paralela a
3x+2y+7=0
será una recta de la forma
3x+2y+c = 0
Y ahora debemos hallar las rectas de esa forma que tienen un solo punto de corte con la elipse.
$$\begin{align}&3x+2y+d=0 \implies x=-\frac{2y+d}{3}\\&\\&\frac {x^2}{10}+\frac{(2y)^2}{5}=1\\&\\&\frac{\frac{4y^2+4yd+d^2}{9}}{10}+\frac{4y^2}{5}=1\\&\\&\frac{4y^2+4yd+d^2}{90}+\frac{72y^2}{90}=1\\&\\&76y^2+4yd+d^2=90\\&\\&76y^2+4yd+d^2-90=0\\&\\&\text{Para que haya una solo solución debe}\\&\text{ser 0 el discriminante }b^2-4ac\\&\\&16d^2-4·76(d^2-90)=0\\&\\&16d^2 - 304d^2+27360 = 0\\&\\&288d^2 = 27360\\&\\&d^2= 95\\&\\&d=\pm \sqrt{95}\\&\\&\text{Luego las dos rectas son}\\&\\&3x+2y + \sqrt {95}=0\\&3x+2y-\sqrt{95}=0\\&\end{align}$$Esta es la gráfica, las ecuaciones son las mismas que calculé, pero Geogebra las pone a su forma.
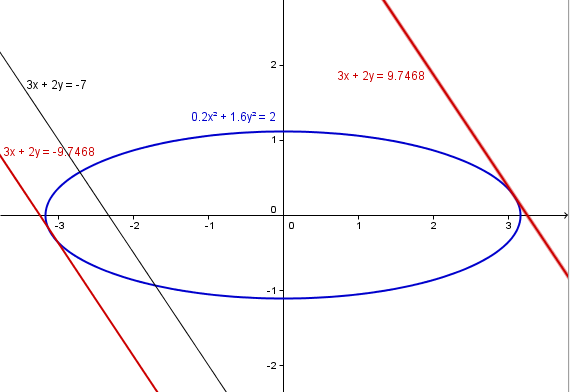
Y eso es todo.
