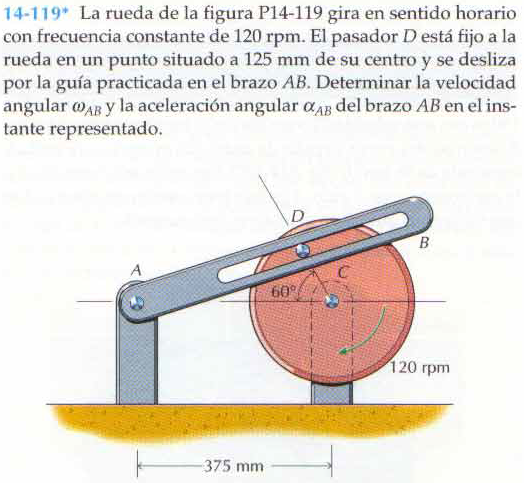
$$\begin{align}& \end{align}$$¡Hola Enrique!
·
Situemos el origen en el punto A que sobre el que gira la varilla.
El centro de la circunferencia será el punto (375,0)
El radio de la circunferencia es 125mm por lo que la ecuación de la circunferencia es
x = 375 + 125·cos(alfa)
y = 125 sen(alfa)
Las 120 rpm vamos a dejarlas mejor en 2 rps (revoluciones por segundo) y el tiempo lo mediremos en segundos
El ángulo alfa del pasador depende del tiempo, si ponemos 2·pi·t dará una vuelta por segundo, como son dos vueltas pondremos 4·pi·t
Con esto la ecuación del pasador es:
x= 375 + 125·cos(4·pi·t)
y = 125sen(4·pi·t)
y el ángulo theta que formará la varilla respcto a OX+ será
$$\begin{align}&w(t)=\frac{2\pi(1+3(-0.5))}{125(5+3(-0.5))}=\frac{-\pi}{437.5} rad/s\end{align}$$El instante que muestra la figura es cuando 4pi·t = 120º = 2pi/3
Pero lo único que nos interesa es que el coseno es -1/2
Luego la velociada angular será:
$$\begin{align}&w(t)=\frac{2\pi(1+3(-0.5))}{125(5+3(-0.5))}=\frac{-\pi}{437.5} rad/s\end{align}$$Me parece muy baja luego estará mal, pero el ordenador anda medio bloqueado y mando esto antes de que se pierda todo el trabajo. Espera que continue el ejercicio.