Derivadas: halle la ecuación de Lt

Tal como la has escrito sería la primera:

$$\begin{align}&y=\sqrt x + \frac{1}{x}\\&\\&y'=\frac{1}{2 \sqrt x}-\frac{1}{x^2}\\&\\&m=y'(1)=\frac{1}{2}-1=-\frac{1}{2}\\&\\&f(1)=\sqrt 1 + \frac{1}{1}=2\\&\\&Punto \ Tangencia (1,2)\\&pendiente \ recta \ tangente \ m=-\frac{1}{2}\\&L T\\&y-y_o=m(x-x_o)\\&\\&y-2=-\frac{1}{2}(x-1)\end{align}$$

·

Hay que usar parénteis para indicar las operaciones que se hacen primero, máxime cuando estás poniendo una raíz cuadrada, una suma y una división que no tienen nada de conmutativas ni de asociativas entre sí. Hay varias interpretaciones posibles. La primera sería la oficial, la que te interpretaría un ordenador o una persona conocedera de las reglas, yluego hay otras que es muy posible sean la real pero no has sabido expresarla

$$\begin{align}&a)\quad \sqrt x+\frac 1x\\&\\&b)\quad  \frac{\sqrt {x+1}}{x}\\&\\&c)\quad  \sqrt{\frac{x+1}{x}}\end{align}$$

Voy a calcular la tangente para la situación b) ya que la a) ya te la han resuelto.  Si en realida es la b) deberías haber escrito

f(x) = sqrt(x+1) / x

Lo de sqrt(...) es la raíz cuadrada de lo que hay dentro

$$\begin{align}&\text{La ecuación dela recta tangente a f(x) en }(x_0,y_0) \;es:\\&\\&y=y_0+f'(x_0)(x-x_0)\\&\\&f(x)=\frac{\sqrt{x+1}}{x}\\&\\&x_0=1\implies y_0=f(x_0)=\frac{\sqrt {1+1}}{1}=\sqrt 2\\&\\&(x_0,y_0)=(1, \sqrt 2)\\&\\&f'(x)=\frac{\frac{1}{2 \sqrt {x+1}}·x-\sqrt{x+1}}{x^2}=\\&\\&\frac{x-2x-2}{2x^2 \sqrt{x+1}}=\frac{-x-2}{2x^2 \sqrt{x+1}}\\&\\&f'(x_o)=f'(1)=\frac{-3}{2 \sqrt 2}=\frac{-3 \sqrt 2}{4}\\&\\&\text{Y la tangente es}\\&\\&y= \sqrt 2-\frac{3 \sqrt 2}{4}(x-1)\\&\\&y= -\frac{3 \sqrt 2}{4}x +\frac{7 \sqrt 2}{4}\\&\\&\text{o si lo prefieres}\\&\\&y=\frac{\sqrt 2}{4}(7-3x)\end{align}$$

Y esta es la gráfica.

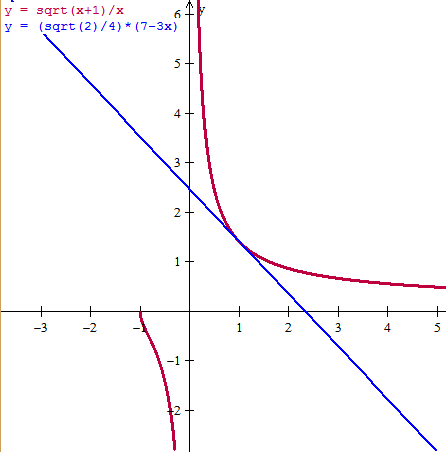
Y eso es todo, pero antes de nada fíjate en si he usado la función que tienes u otra. Si no has entendido algo pregúntame. Y si ya está bien, no olvides puntuar.