Hallar la gráfica de la hipérbola definida como funcion

·

La ecuación de la hipérbola es similar a la e la elipse pero con un signo -. Lo que ya no tengo tan claro es lo que pasa cuando no salen los focos en la línea horizontal pero ya se investigará si se da el caso.

La forma canónica es

$$\begin{align}&\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}=1\\&\\&\text{Y la ecuación de la hipérbola es}\\&\\&x^2-y^2+2y-5=0\\&\\&x^2 -(y^2-2y)-5=0\\&\\&\text{Completamos cuadrados}\\&\\&x^2 -[(y-1)^2-1]-5=0\\&\\&x^2-(y-1)^2+1-5=0\\&\\&x^2 -(y-1)^2 = 4\\&\\&\frac{x}{2^2}-\frac{(y-1)^2}{2^2}=1\end{align}$$

Es una hipérbola equilátera ya que a=b.

El centro es (0,1)

Las asíntotas tienen pendiente b/a y -b/a es decir 2/2 y -2/2, 1 y -1.

Para que pasen por el centro que es (0,1) deben ser

y=x+1

y=-x+1

La distancia focal en la hipérbola es la raíz cuadrada de a^2 + b^2

c= sqrt(4+4) = sqrt(8) = 2·sqrt(2) = 2.8247125

Dibujaremos esos focos a esa distancia horizontal del centro. Y a distancia a=2 del centro estarán los vértices. La cajita es un cuadrado 2a x 2b centrado en el centro y c es la linea del centro de un lado al centro del siguiente.

Y con esos datos yo creo que es suficiente para dibujarla.

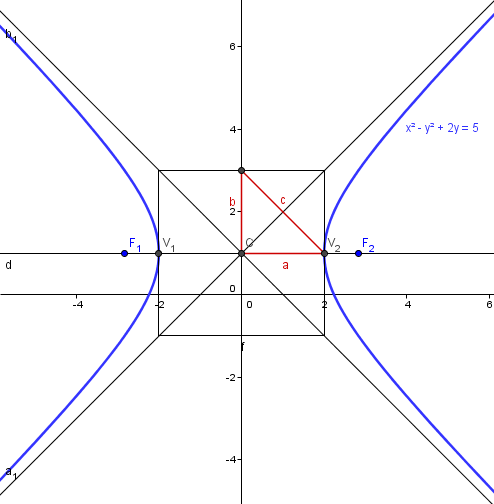
Y eso es todo.