¿De que forma puedo calcular el área de este recinto? : : -

$$\begin{align}& \end{align}$$

¡Hola Alberto!

·

Hay que hacer la gráfica para enterarse de algo.

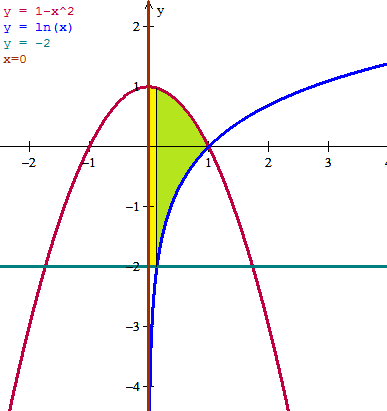
Ha habido que tener cuidado para no equivocarse con la región.

Vemos que serán necesarias dos integrales una par la región amarilla y otra para la verde. Debemos calcular los límites de estas integrales

La primera empieza en 0 y termina donde

ln(x) = -2

x=e^(-2)

La segunda empieza en e^(-2) y termina en

ln(x) = 1-x^2

Gracias a Dios que se ve y puede comprobarse que es x=1, porque si no no es una ecuación resoluble fácilmente.

Entonces el área es:

$$\begin{align}&A=\int_0^{e^{-2}}(1-x^2-(-2))dx+\int_{e^{-2}}^1(1-x^2-lnx)dx=\\&\\&\int_0^{e^{-2}}(3-x^2)dx+\int_{e^{-2}}^1(1-x^2-lnx)dx=\\&\\&\text{hago aparte la integral de ln x, lo demás es inmediato}\\&\\&\int ln\,dx=\\&u=ln\,x\qquad du=\frac{dx}{x}\\&v=dx\qquad\;\;\; v=x\\&=x\,ln\,x-\int dx = x\,ln\,x-x\\&\\&=\left[3x-\frac{x^3}{3}  \right]_0^{e^{-2}}+\left[x-\frac{x^3}3 -x\,ln\,x+x \right]_{e^{-2}}^1=\\&\\&3e^{-2}-\frac{e^{-6}}{3}+1-\frac 13-0+1-e^{-2}+\frac{e^{-6}}{3}+e^{-2}(-2)-e^{-2}=\\&\\&-e^{-2}+\frac 53\\&\\&\text{Esa es la respuesta real, si quieres saber su valor aproximado es}\\&\\&\approx 1.531331383\end{align}$$

Y eso es todo.