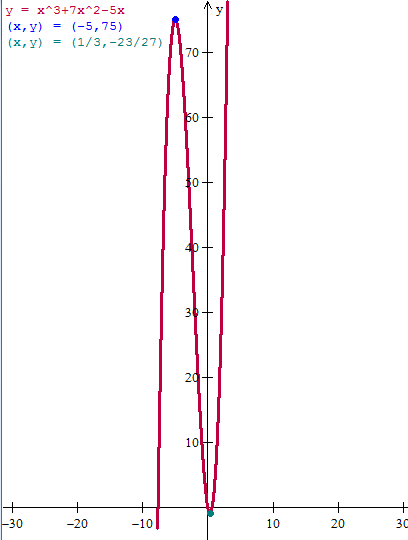
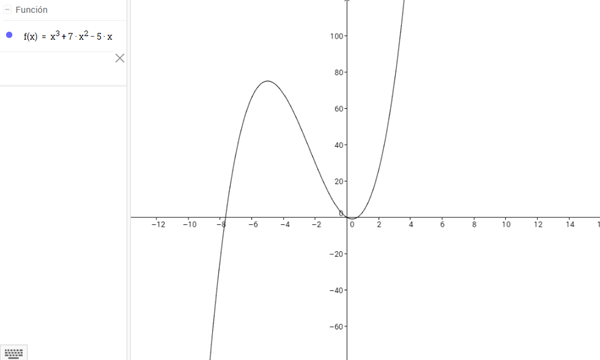
¿Ejercicio Resuelve el siguiente ejercicio dada f(x)= ?
- a) Los valores críticos.
- b) Los intervalos donde f (x) es creciente o decreciente.
- c) Los valores máximos y mínimos.
- d) La gráfica de la función.
2 Respuestas
Respuesta de Valero Angel Serrano Mercadal
1
·
Los valores críticos son aquellos donde no existe la derivada o donde existe y es 0.
Esta función es ferivabel en todo R, los valores críticos solo son los que la derivada es 0
f(x) = x^3+7x^2-5x
f'(x) = 3x^2 + 14x - 5
calculamos las raíces
$$\begin{align}&x=\frac{-14\pm \sqrt{14^2+60}}{6}=\\&\\&\frac{-14\pm 16}{6}= -5\; y\;\frac 13 \\&\\&\text{2) Como f'(x) es una parábola hacia arriba}\\&\\&(-\infty,-5) \quad f'(x)\gt0\implies f(x)\; creciente\\&\left(-5,\frac 13\right)\quad f'(x)\lt0\implies f(x)\;decreciente\\&\left(\frac 13,\infty\right)\quad f'(x)\gt0\implies f(x)\;creciente\\&\\&\text{3) A -5 llega f(x) creciendo luego es un máximo}\\&\text{a 1/3 llega decreciendo, luego es un mínimo}\\&\\&\text{El maximo es:}\\&f(-5)=(-5)^3+7(-5)^2-5(-5) =\\&-125+175+25 = 75\\&\\&\text{El mínimo es}\\&f\left(\frac 13 \right)=\left(\frac 13 \right)^3+7\left(\frac 13 \right)^2-5\left(\frac 13 \right)=\\&\\&\frac 1{27}+\frac 79-\frac 53=\frac{1+21-45}{27}=-\frac{23}{27}\\&\\&\end{align}$$4) Y la gráfica es esta:
¡Hla Yisus!
Pregunta con varios apartados y con gráfica resuelta a la perfecección por los dos que te hemos contestado. ¿A qué esperas para votar excelente? Desde luego que por mi parte ya puedes esperar toda la vida, no te contestaré más preguntas mientras no cambies la puntuación de esta a Excelente.
Respuesta
1
Veamos...
$$\begin{align}&f(x) = x^3 + 7x^2 -5x\\&\mbox{No lo piden, pero también vamos a calcular los ceros de la función, para eso vamos a escribir f(x) de otro modo}\\&f(x) = x(x^2 + 7x -5)\\&\mbox{Mediante la cuadrática podemos resolver esa ecuación que queda de grado 2}\\&\mbox{Las raíces son: }\frac{-7\pm \sqrt{69}}{2} \\&x_1 \approx 0,6533 \land x_2 \approx -7,6533\\&f(x) = x(x-0,6533)(x+7,6533)\\&\mbox{Ahora sí, vamos a calcular lo que piden, para eso calculamos f'(x) y f''(x)}\\&f'(x) = 3x^2 + 14x -5\\&f''(x)= 6x + 14\\&f'(x)=0 \to x_1=1/3 \land x_2=-5 \ (puntos\ ríticos)\\&f''(-5) = 6*(-5)+14 < 0 \to máximo\\&f''(1/3) = 6*1/3+14 > 0 \to mínimo\\&\lim_{x \to -\infty} f(x) \to -\infty\\&\lim_{x \to +\infty} f(x) \to +\infty\\&\mbox{La función crece hasta el máximo en -5, luego decrece hasta el mínimo en 1/3 y luego vuelve a crecer}\\&\mbox{En concecuencia, los intervalos de crecimiento/decrecimiento son:}\\&Crece: (-\infty, -5)\ U\ (1/3, +\infty)\\&Decrece:(-5, 1/3)\\&\end{align}$$Y la gráfica sería (aunque supongo que te la piden que la hagas "a mano"):
