Tarea de Máximos, mínimos, hallar max y min de una función
Estoy entendiendo más el procedimiento con los pasos a seguir.
Necesito saber como hallar los máximos y mínimos de esta función f(x)=x^3-3x^2-9x+15, es para entregar mi evidencia hoy ojala que puedan aun ayudarme ^_^
1 Respuesta
·
Pues lo mismo que en los tros ejercicios, se deriva, se iguala a 0 y se calculan las raíces, luego se comprueba el signo de ellas en la derivada segunda.
f(x)=x^3 - 3x^2 - 9x+15
f'(x) = 3x^2 - 6x - 9 = 0
Para facilitar un poco las cuentas podemos calcular las raíces de la derivada dividida por 3
x^2 - 2x - 3 = 0
Esta ecuación se factoriza de cabeza
x^2 - 2x - 3 = (x+a)(x+b) = x^2 + (a+b)x + ab
luego
ab = -3
a+b = -2
y lo que decía, de cabeza se ve que
a=-3
b=1
x^2 - 2x - 3 = (x-3)(x+1)
las raíces son 3 y -1
Calculamos la derivada segunda, antes recuerdo que la primera era
f'(x) = 3x^2 - 6x - 9
f''(x) = 6x -6
Y veamos el signo de las raices en esta derivada segunda
f''(3) = 6·3 - 6 = 12>0 luego es mínimo
f''(-1) = 6·(-1) -6 = -6 -6 = -12 <0 luego es máximo
Y los valores de la función son
f(x)=x^3 - 3x^2 - 9x + 15
f(3)=3^3 - 3·3^2 - 9·3 + 15 = 27-27-27+15 = -12
f(-1)=(-1)^3 -3·(-1)^2 -9·(-1) + 15 = -1-3+9+15 = 20
Asi el mínimo relativo es (3, -12)
Y el máximo relativo es (-1, 20)
Esta es la gráfica.
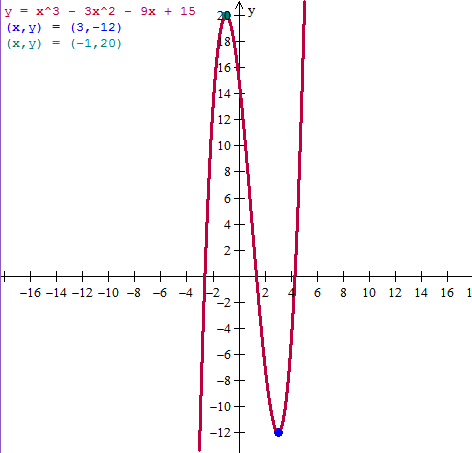
Y eso es todo.
