Cómo resolver este ejercicio y realizar su gráfica.
Hallar
$$\begin{align}&dy\over dx\end{align}$$y las pendientes de las rectas tangentes mostradas en la gráfica de la ecuación en polares.
Siguiendo la expresión a que llegara Gustavo Omar ...
r= 2 + 3 sen( theta) ...............y aplicando el desarrollo.................................
para cada uno de los puntos indicados en la curva seria:
Para( 5 , pi/2) ............................dy/dx= 0 + 5x0 / 3 x 0 - 3x1 = 0
Para ( 2 , pi) ................................dy/dx= 0 + -2 / 3 + 0 = - 2/3 .......pendiente = -33.7°
Para ( 1 , 3pi/2) ............................dy/dx = 0+0 / 0 +1= 0
Para ( 2 , 0) ...................................dy/dx= 0 + 2 / 3 - 0 = 2/3 ..,....pendiente= 33.7°
Me estoy basando en el punto " Calculo Diferencial" del link:
1 respuesta más de otro experto
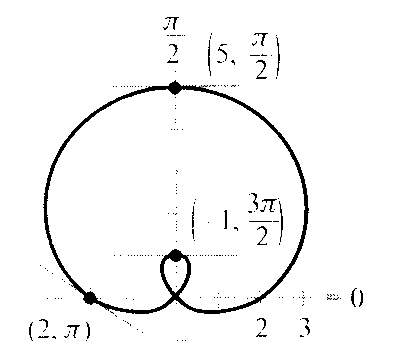
Tenemos 4 puntos, así que voy a intentar escribir una ecuación genérica para intentar deducir la expresión general
$$\begin{align}&Intentaré\ hallar\ r=f(\theta)\\&General\\&r=a + b\ sen(\theta+c) + d\ \cos(\theta)\\&Ahora,\ reemplazaré\ los\ valores\ que\ tenemos:\\&5 = a+b sen(\pi/2 + c)+ d \cos(\pi/2)\\&2 = a+b sen(\pi + c)+ d \cos(\pi)\\&1 = a+b sen(3 \pi/2 + c)+ d \cos(3 \pi/2)\\&2 = a+b sen(0 + c)+ d \cos(0)\\&\text{Voy a evaluar los cosenos...}\\&5 = a+b sen(\pi/2 + c)\\&2 = a+b sen(\pi + c)- d\\&1 = a+b sen(3 \pi/2 + c)\\&2 = a+b sen( c)+ d\\&Sabiendo\ que\ sen(\alpha + \beta)=sen(\alpha)\cos(\beta) + sen(\beta)\cos(\alpha)\\&5 = a+b \cos(c)\\&2 = a-b sen(c)- d\\&1 = a-b \cos(c)\\&2 = a+b sen( c)+ d\\&\text{Sumando las ecuaciones 1 y 3 por un lado y 2, 4 por otro, se llega a que}\\&a=4 \ y\ a=6, \text{lo que no puede ser, así que asumo que la tercer ecuación no se ve el signo }\\&\text{negativo y en realidad el punto dado es en realidad }(-1, \frac{3}{2} \pi)\text{, quedando de este modo las siguientes ecuaciones}\\&5 = a+b \cos(c)\\&2 = a-b sen(c)- d\\&-1 = a-b \cos(c)\\&2 = a+b sen( c)+ d\\&\text{ahora sí, sumando (1)+(3) ó (2)+(4), llegamos a: } a=2\\&Reescribimos, \ reemplazando\ lo\ conocido\\&3 = b \cos(c)\\&0 = -b sen(c)- d\\&-3 =-b \cos(c)\\&0 = b sen( c)+ d\\&\text{Quedan dos ecuaciones equivalentes a las otras dos, así que podemos quedarnos con}\\&3 = b \cos(c)\\&0 = b sen(c)+d\\&\text{Tengo mas incognitas, que ecuaciones, asumo:}\\&b=3, c=0 \text{que cumple la primer ecuación} yqueda\\&0 = 3 sen(0) +d \to d=0\\&\text{por lo tanto los valores son:} a=2,b=3,c=0,d=0 \text{, quedando la expresión original}\\&r=2+3sen(\theta)\\&\\&\\&\\&\\&\end{align}$$Dejo la solución hasta acá, porque:
1) Me tengo que ir
2) No confío en el editor de texto de esta página
Intenta avanzar desde acá, igualmente luego veré de seguir esta pregunta
Acá estoy de nuevo... la verdad que no me queda fácil de despejar la ecuación para que quede y=f(x), pues sucede que para transformar de Polar a Rectangular debemos hacer...
$$\begin{align}&\text{Sabiendo que la transformación que hay que hacer viene dada por:}\\&r=\sqrt{x^2+y^2}\\&\theta=arctan(\frac{y}{x})\\&\text{y recordando que la ecuación que teníamos es:}\\&r=2+3sen(\theta)\\&\sqrt{x^2+y^2}=2+3sen(\theta)\\&\sqrt{x^2+y^2}=2+3sen(arctan(\frac{y}{x}))\\&x^2+y^2=\bigg(2+3sen(arctan(\frac{y}{x}))\bigg)^2\\&y^2=\bigg(2+3sen(arctan(\frac{y}{x}))\bigg)^2-x^2\\&y=\sqrt{\bigg(2+3sen(arctan(\frac{y}{x}))\bigg)^2-x^2}\\&\\&\\&\\&\\&\end{align}$$El tema es que queda "y" a ambos lados de la ecuación y no encuentro una forma algebraica de despejarla,...