$$\Begin{align}& \end{align}$$Lo primero es hacer una imagen de la situación, como soy malo dibujando (y más de forma digital), voy a intentar bosquejar mi dibujo y te recomiendo que intentes hacer lo mismo.
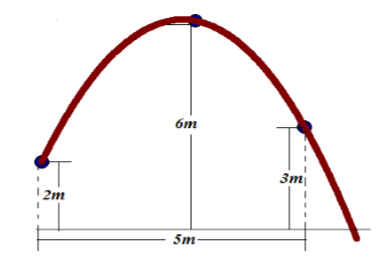
Voy a poner el origen de coordenadas en los pies del jugador, de esta forma la información relevante que tenemos es:
Se lanza desde el punto (0,2), así que tenemos
x_0 = 0 y_0 = 2 m
El aro está a 3 m de altura y a 5m de distancia del jugador, así que está en el punto (5,3)
La altura máxima del balón es de 6m y lo que nos piden es calcular para que valor de x se da esta situación.
Ahora voy a plantear las ecuaciones del "tiro parabólico"
$$\begin{align}&x(t) = x_0 + v_{x0} t + 1/2 a_x t^2\\&y(t) = y_0 + v_{y0} t + 1/2 a_y t^2\\&v_x(t) = v_{x0} + a_x t\\&v_y(t) = v_{y0} + a_y t\\&\text{y reemplazando los datos que tenemos conocidos en este ejercicio, nos queda}\\&x(t) = v_{x0} t\\&y(t) = 2 + v_{y0} t - 1/2 g t^2\\&v_x(t) = v_{x0}\\&v_y(t) = v_{y0} - g t\\&\text{ Sabemos que la altura (y=6m) será máxima cuando la velocidad en y sea 0, luego}\\&6 = 2 + v_{y0} t - 1/2 g t^2...........................(1)\\&0 = v_{y0} - g t \to t=\frac{v_{y0} }{g}.........................(2)\\&Reemplazando \ (2)\ en\ (1)\\&4 = v_{y0} \cdot \frac{v_{y0} }{g} - 1/2 g (\frac{v_{y0} }{g})^2\\&4 = \frac{(v_{y0})^2 }{g} - \frac{(v_{y0})^2 }{2g}\\&4 = \frac{2(v_{y0})^2-(v_{y0})^2}{2g}\\&8g = (v_{y0})^2\\&Considerando\ g = 9.8 m/s^2 \\&v_{y0}=\sqrt {8g}=\sqrt{8 \cdot 9.8}=8.85\ m/s\\&Reemplazo\ en\ (2)\\&t=\frac{v_{y0} }{g}=\frac{8.85}{9.8}=0.9\ s\\&\text{O sea que sabemos que la altura máxima se da a los 0.9 seg; para calcular x nos está faltando la velocidad inicial en este sentido, para esto vamos a usar alguna propiedad de la parábola}\\&\text{como el máximo se da en 0.9; al doble de ese tiempo estará a la misma altura que en el inicio (y=2m)}\\&\text{Veamos además a que tiempos la altura de la pelota es 3m (esto nos ayudará a calcular }v_{x0})\\&y(t)=3 \to 3=2+8.85 t - 1/2 g t^2\\&0=-1+8.85 t - 1/2 g t^2\\&t_1=0.12 s \ \text{(mientras la pelota va subiendo)}\\&t_2=1.685 s\ \text{(mientras la pelota baja -en el aro)}\\&\text{además sabemos que en 1.685s la pelota está en x=5m, usemos esto...}\\&x=5m = v_{x0} 1.685\\&v_{x0}=\frac{5}{1.685}=2.97 m/s\\&\text{Ahora sí, usemos este valor para ver cual es la distancia donde la altura fue maxima, antes voy a escribir nuevamente todas las ecuaciones, pero reemplazando todos los valores que tenemos}\\&x(t) = 2.97 \ t\\&y(t) = 2 + 8.85\ t - 4.9\ t^2\\&v_x(t) = 2.97\\&v_y(t) = 8.85 - 9.8\ t\\&ahora\ si:\\&x(0.9)=2.97 \cdot 0.9= 2.67m\end{align}$$

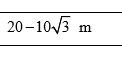
Hola Gustavo... una pregunta... para simbolizar y desarrollar ecuaciones, derivadas, integrales.. etc. ¿utilizas algún programa especial?... ¿Me podrías asesorar al respecto? .Gracias y Saludos. - albert buscapolos Ing°
No Alberto, lo que uso directamente es el editor de LaTex (el anteúltimo icono que aparece en la barra cuando estás respondiendo, que tiene un símbolo de X al cuadrado), la verdad que no es muy bueno, pero entre eso y la ayuda (y bastante paciencia), se puede escribir bastante bien :)Saludos! - Anónimo
Gracias...gustavo..!! - albert buscapolos Ing°