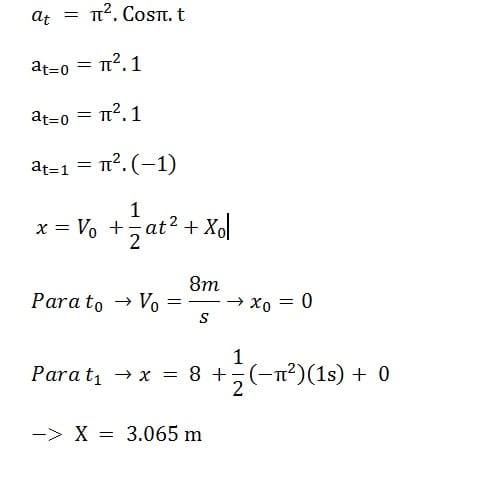Problema de aceleración de una partícula para resolver con integrales
Buenas tardes sigo con mi taller ya casi termino les agradezco su ayuda es fundamental para mi estudio a distancia
2 Respuestas
Respuesta de Valero Angel Serrano Mercadal
3
·
·
¡Hola Oscar!
No sirve la fórmula del espacio que han usado en la otra respuesta. Esa fórmula es valida cuando la aceleración es constante (movimiento unifórmemente acelerado), se deduce de integrar dos veces la constante llamada a. Pero si la aceleración no es una constante, el espacio es la integral segunda de la función aceleración, y no tiene por que dar nada parecido a esa fórmula.
$$\begin{align}&v(t)=\int a(t) dt\\&\\&v(t)=\int \pi^2cos(\pi t)\;dt=\pi \,sen(\pi t)+C\\&\\&\text{Como }v(0)=8\\&\\&8=v(0)=\pi\, sen(\pi·0)+C = 0+C =C\\&C=8\\&\\&v(t)=\pi\,sen(\pi t)+8\\&\\&\\&s(t)=\int v(t) dt\\&\\&s(t)=\int (\pi\,sen(\pi t)+8)dt=\\&\\&-\cos(\pi t)+8t+C\\&\\&\text{Como } s(0)=0\\&\\&0=s(0)=-\cos(\pi·0)+8·0+C=-1+C\\&\\&C=1\\&\\&Luego\\&\\&s(t)= -\cos(\pi t)+8t + 1\\&\\&\text{por lo tanto para t=1}\\&\\&s(1) = -\cos(\pi)+8(-1)+1=-1-8+1=-8m\end{align}$$:
:
