Como podría realizar este ejercicio de dinámica, para calcular la aceleración con una gravedad de -10m/seg^2 3ra ley de newton
3ra ley de newton plano inclinado
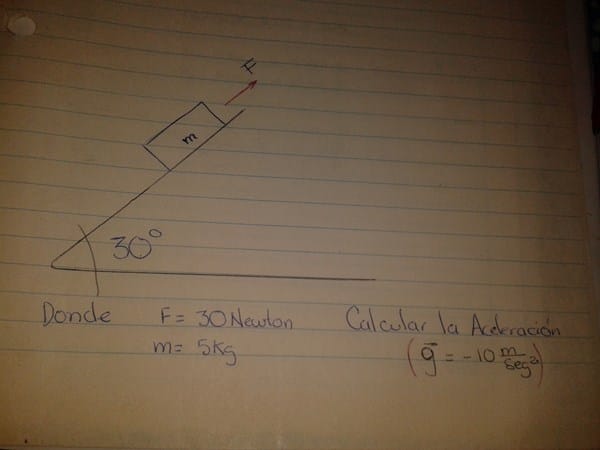
Como podría realizar este ejercicio de dinámica, para calcular la aceleración con una gravedad de -10m/seg^2
esa es mi duda ya que a=g=-10m/seg^2 y estoy confusa al realizarlo
Mantengo un angulo de 30grados
Fuerza de 30Newton
Masa de 5kg
g=-10m/seg^2
Debo calcular la aceleracion
Desearia que me pudiesen ayudar a plantear mi formula para poder resolverlo
Respuesta de albert buscapolos Ing°
1
1 respuesta más de otro experto
Respuesta de Valero Angel Serrano Mercadal
1

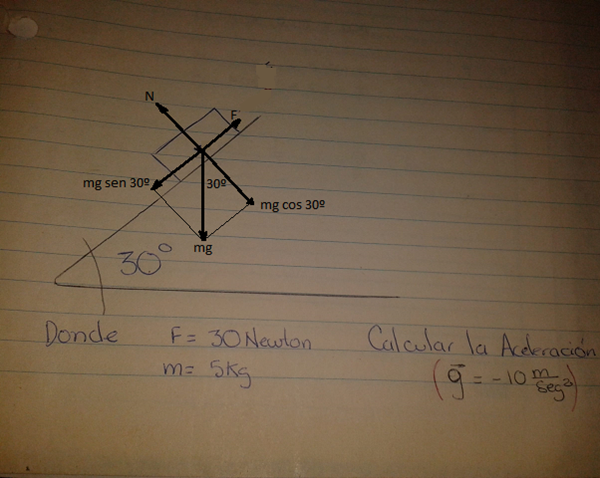
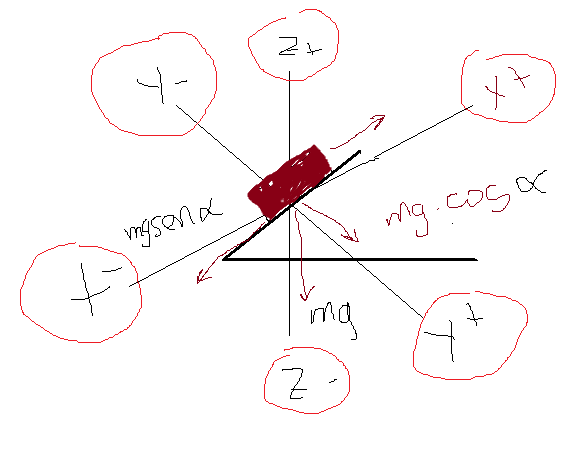
Creo que no has tenido en cuenta la fuerza de 30 N que se ejerce hacia arriba paralela al plano inclinado. - Valero Angel Serrano Mercadal
Oh.....asi es ! - albert buscapolos Ing°