Problema de calculo de áreas de una curva

·

·

¡Hola Ana!

Haremos primero la curva que es gran ayuda.

Calcularemos algebraicamente los puntos de intersección. Igualamos las dos funciones.

(x-1)^2=x+1

x^2 - 2x +1 = x+1

x^2 - 3x = 0

x(x-3)=0

las intersecciones son

x=0,  x=3

Esos son los límites de integración. Además vemos que la recta está por encima, luego sera el minuendo.

$$\begin{align}&A=\int_0^3 (x+1-(x-1)^2)dx=\\&\\&\int_0^3(x+1-x^2+2x-1)dx=\\&\\&\int_0^2(3x-x^2)dx=\left[\frac {3x^2}2-\frac {x^3}{3}\right]_0^3=\\&\\&\frac{27}{2}-9=\frac 92\end{align}$$

:

:

Lo siento está mal porque los límites de integración que puse eran los que delimitaban entre las curvas y los que piden son otros. Pero ahora tengo que dejar el ordenador muchas horas y no lo puedo corregir.

Saludos.

:

:

Ya veo que la han cotestado, pero yo tenía pendiente corregirla así que voy a hacerlo.

Esta es la gráfica de lo que nos piden

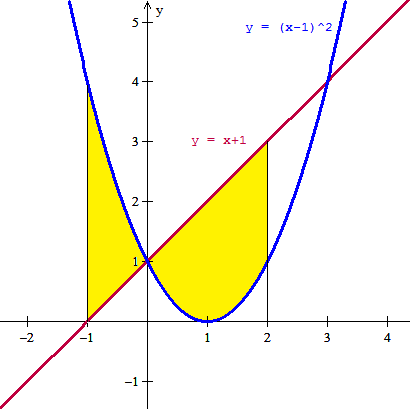
Como vemos el área es la suma de la de dos regiones.  En la gráfica se ve claro que las dos funciones se cortan en x=0 pero eso hay que calcularlo algebraicamente y ya lo habíamos hecho antes, nos daba que se cortaban en 0 y 3.  Como el intervalo del área es [-1, 2]  solo entra dentro el corte en x=0 y eso hace que haya dos zonas en las que debemos calcular independientemente el área. La vez anterior te llené de valores absolutos y lo aperé todo a la vez. Yo creo que será más claro si lo hacemos individualmente.

Lo primero calculamos la integral indefinida de la diferencia de funciones porque eso sirve para calcular las dos áreas. Ya le tenía hecha de antes, simplemente la copio

$$\begin{align}&\int (x+1-(x-1)^2)dx=\\&\\&\int(x+1-x^2+2x-1)dx=\\&\\&\int(3x-x^2)dx=\frac {3x^2}2-\frac {x^3}{3}\\&\\&\text{El área de la región izquierda será el valor absoluto}\\&\text{de la definida entre -1 y 0}\\&\\&A_I=\left|0-0-\frac {3·(-1)^2}2+\frac {(-1)^3}3  \right|=\left|\frac 32-\frac 13  \right|=\\&\\&\left|\frac{-9-2}{6}  \right|=\frac {11}6\\&\\&\text{Y la de la derecha es lo mismo entre 0 y 2}\\&\\&A_D=\left|\frac{3·2^2}{2}-\frac {2^3}3-0+0  \right|=\left|6-\frac 83  \right|=\frac{10}3\\&\\&\\&A=A_I+A_D=\frac {11}6+\frac{10}3=\frac{11+20}{6}=\frac{31}{6}\end{align}$$

:

:

Disculpe por que en mi gráfica dice que el área es 1.5 si 31/6=5.5

Para empezar 31/6 = 5.1666... pero eso es lo menos importante.

Estamos de acuerdo en la respuesta Gustavo, yo y el programa que suelo emplear siempre para comprobar que la respuesta está bien. Tengo una idea:

Si hiciera la integral toda de una vez sería:

$$\begin{align}&\left[\frac {3x^2}2-\frac {x^3}{3}\right]_{-1}^2=6-\frac 83-\frac 32-\frac 13 =\frac 32=1.5\end{align}$$

Ahí tienes la respuesta.  Han hecho la integral de un tirón sin darse cuenta que las funciones se cruzaban y tenían que tomar los valores absolutos del área de cada lado, lo que han hecho no ha sido sumar las áreas sino restarlas.

Y eso es todo, saludos.

·

·

¡Gracias! de verdad le agradezco mucho la ayuda

Aunque el maestro que me corrigió dice que esta mal por que La integral de 1 dx es por, en este caso no lo esta agregado y que es por eso no sale la operación, checalo.

Aunque el maestro que me corrigió dice que esta mal por que La integral de 1 dx es x, en este caso no lo esta agregado y que es por eso no sale la operación, checalo