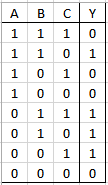
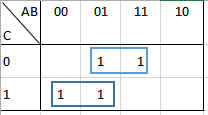
Tengo un Problema de expresión booleana
Estoy viendo álgebra booleana pero no entiendo bien, creo que lo que entiendo es como realizar el circuito equivalente, pero no entiendo como minimizar la expresión ni como se realiza la tabla, me podrían ayudar!
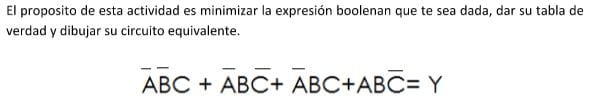
3 Respuestas
·
·
La tabla de verdad de esa expresión es aquella que es verdadera para los minitérminos que aparecen en ella y falsa para los otros.
Y ahora yo no sé como hacéis el circuito equivalente, si simplificando la expresión con las propiedades de las operaciones o mediante diagramas de Karnaugh
Ya me lo dirás.
Saludos.
:
:
creo que entiendo en la tabla esta abc=y, y eso es la indicación de la reducción,
solo una pregunta que forma sigue para reducción de términos?
Puedes reducir por propiedades:
Hay una propiedad que es:
XY + XY' = X
Entonces tenemos los términos primero y tercero
A'B'C + A'BC = (A'C)B' + (A'C)B = A'C
segundo y tercero
(A'B)C' + (A'B)C = A'B
segundo y cuarto
A'(BC') + A(BC') = BC'
Y otra propiedad es
X+X=X
por la cual podemos repetir los términos que queramos y queda igual
primero+segundo+tercero+cuarto=
(primero+tercero)+(segundo+tercero)+(segundo+cuarto)=
A'C+A'B + BC'
5 puertas
Y yo no veo más simplificación salvo si acaso esta
A'(C+B) +BC'
4 puertas
Y eso es todo, saludos.
:
:
¡Gracias! de verdad busque y no encontré algo conciso para aprender y analizar
Como no dijiste nada cuando te pregunte por los diagramas de Karnaugh pensaba que no los habíais dado y por eso no los usé. Pero al menos podría haber comprobado si mi resultado estaba bien simplificado o no.
Este es el diagrama de Karnaugh
Y efectivamente, se ve que la simplificación buena es
Y= A'C + BC'
Sin lo diagramas de Karnaugh es difícil llagar a esas simplificaciones, por ejemplo al resultado que obtuve yo
Y = A'C + A'B + BC'
habría que añadirle que A'B = A'BC + A'BC', entonces
Y = (A'C + A'BC) + (A'BC' + BC')
y por absorción
Y = A'C + BC'
Pero sin diagramas estás muerto. Ya me dirás si los usáis.
Saludos.
:
:
¡Gracias! ya me había entrado la duda!
Y ahora que veo la resolución de Mario me doy cuenta que no elegí bien los emparejamientos, si los hubiera elegido así se hacía en pocos pasos. Pero es que la forma de ver bien todo eso es con los diagramas.
La Tabla me da similar a Prof. Valero.
La reduccion x Karnaugh me estaria dando Y = BC* + A*C...............
dos "AND" + una "OR".
-O0o-
Efectivamente Breda y como indica Alberto, la reducción a su mínima expresión de:
Y = A'B'C + A'BC' + A'BC + ABC'
es:
Y = A'C + BC'
_____________________________
Para obtener lo anterior simplemente agrupa:
- El primer y el tercer término, por un lado, y
- El segundo y el cuarto término
Así:
Y = (A'B'C + A'BC) + (A'BC' + ABC')
En cada uno de estos grupos puedes obtener un factor común:
Y = A'C (B' + B) + BC' (A' + A)
Quedando finalmente el resultado apuntado.
Saludos, Mario R.
-O0o-
-O0o-