Halle la matriz escalonada de la matriz A y luego determine si es una matriz invertible

·

·

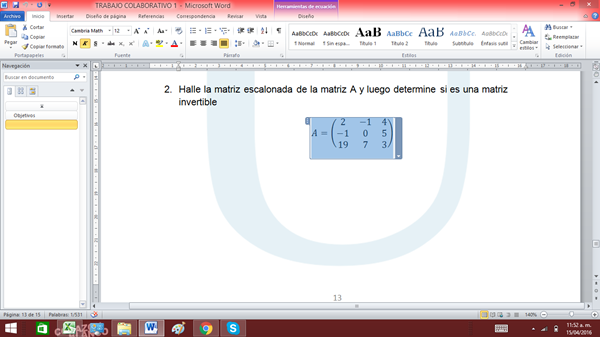
Antes de escalonar una matriz conviene saber para que la queremos escalonar, porque según para que podremos hacer algunas operaciones o no. O si hacemos algunas deberemos llevar un registro de lo hecho.

Por ejemplo, para calcular el rango de una matriz, resolver ecuaciones o comprobar si el determinante es distinto de 0 podemos hacer los tres tipos de operaciones de fila sin ninguna preocupación:

1) Intercambiar filas

2) Multiplicar una fila por una constante distinta de 0

3) Sumar a una fila otro multiplicada por una constante distinta de 0.

Pero si se trata de calcular el determinante solo podemos hacer sin preocupaciones la operación 3. Si se hace la 1 el signo cambia y si se hace la 2 el deteminante queda multiplicado por esa constante.

Como lo que nos piden después es determinar si es invertible y nada más, lo único que necesitamos es averiguar si el determinante es distinto de 0 y podemos hacer cualquiera de las tres.

Luego primero intercambiaré las filas 1 y 2.

-1   0  5

 2  -1  4

19  7  3

No voy a cambiar el signo de la primera fila, me conviene más así como esta para facilitar las operaciones.

Lo siguiente será: A la fila 2 sumare la primera multiplicada por 2. Y a la fila tercera sumaré la primera multiplicada por 19

-1   0    5

 0  -1  14

 0   7  98

Y ahora sumaré la segunda multiplicada por 7 a la tercera

-1   0     5

 0  -1   14

0 0 196

Y ya está escalonada, se podrían hacer más cosas pero esto es suficiente para saber que el determinante es distinto de 0.

Esto que nos da es 196, pero como habíamos intercambiado dos filas, el determinante verdadero es -196 que es distinto de 0, luego la matriz es invertible.

Y eso es todo, saludos.

:

·

:

Veamos como queda porque esta página es pésima para escribir matrices (ni siquiera con el editor de fórmulas quedan bien)

Veamos si podemos escalonar esta matriz

2...... -1....... 4

-1...... 0....... 5 ...(Fila2 = Fila2 + Fila1/2)

19..... 7....... 2 ...(Fila3 = Fila3 - 8.5Fila1)

Próximo paso

2...... -1...... 4

0..... - 1/2.... 7

0..... 31/2.. -31 ...(Fila3 = Fila3 + 31Fila2)

Próximo paso

2...... -1...... 4

0..... - 1/2.... 7

0........ 0 ...186

Quedo triangular superior con los elementos de la diagonal distinto de cero, así que es invertible