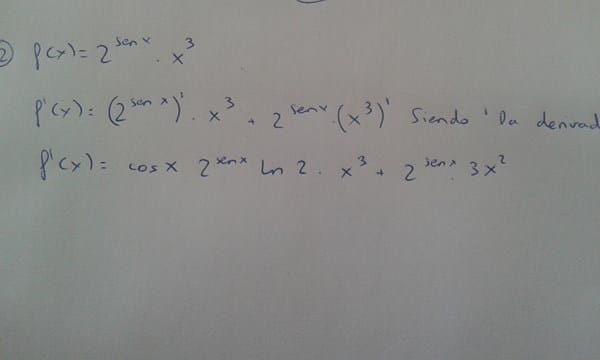Podrían colaborarme con la solución ejercicios de derivadas.
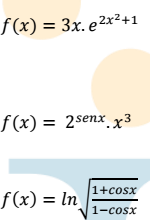
Agradezco su colaboración en la explicación y solución de estos ejercicios
Respuesta de Nicolas Guzman
3 respuestas más de otros expertos
Respuesta de Valero Angel Serrano Mercadal
2
Respuesta
1
Respuesta de Jorge Herrera