Problema de optimización, cono inscrito en esfera de radio R

;)
Hola Carlos!

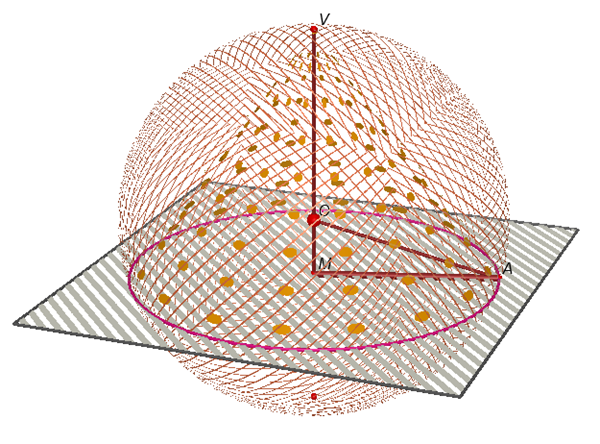
$$\begin{align}&V_{con}=\frac{1}{3} \pi r^2h=f(r,h)\\&VM=h\\&MA=r\\&OV=OA=R\\&OM=VM-VO=h-R\\&\\&OA^2=OM^2+MA^2\\&R^2=(h-R)^2+r^2\\&r^2=R^2-(h-R)^2=R^2-(h^2-2hR+R^2)=2hR-h^2\\&\\&V_{con}(h)=\frac{1}{3} \pi (2hR-h^2)h=\frac{1}{3} \pi (2Rh^2-h^3)\\&DomV(h)=(0,2R)\\&V'(h) \frac{1}{3} \pi (4Rh-3h^2) \Rightarrow V'=0 \\&4Rh-3h^2=0\\&h(4R-3h)=0 \Rightarrow h= \frac{4}{3}R\\&\\&V''(h)= \frac{1}{3} \pi (4R-6h)\\&V''(\frac{4}{3}R)= \frac{1}{3} \pi (4R- \frac{24}{3}R)<0 \rightarrow MAXIMO\\&\\&r^2=2hR-h^2=2 \frac{4}{3}R^2-(\frac{4}{3}R)^2=\frac{8}{9}R^2\\&\\&r=\frac{2 \sqrt 2}{3}R\\&\\&V_{max}= \frac{1}{3} \pi (\frac{8}{9}R^2)( \frac{4}{3}R)=\frac{32 \pi}{81} R^3\\&\\&\frac{V_{conMax}}{V_{esfera}}=\frac{\frac{32 \pi}{81} R^3}{\frac{4}{3} \pi R^3}=\frac{96}{324}=\frac{8}{27} \Rightarrow\\&\\& \%= \frac{8}{27}100=29.6296 \%\end{align}$$