La geometría analítica por medio de la consideración de la circunferencia.
De la siguiente imagen adjunta se menciona la siguiente instrucción a considerar:
·
·
¡Hola Mat cdr!
Ya te dije en esta pregunta que no encuentro justificación a la puntuación. Trabajamos mucho y no deberías escatimar en la puntuación cuando una pregunta está bien respondida. Y Lucas no te ha dicho nada pero piensa lo mismo. Para que te sigamos contestando debes subir la puntuación a Excelente de esta pregunta
La ecuación qué define un lugar geométrico
Sa lu dos.
:
:
Esta es la imagen. Para dibujarla he calculado la mediatriz de un segmento. Sin embargo, creo que analíticamente puede ser más fácil encontrar el centro como el punto de la recta perpendicular que equidista de A y B.
·
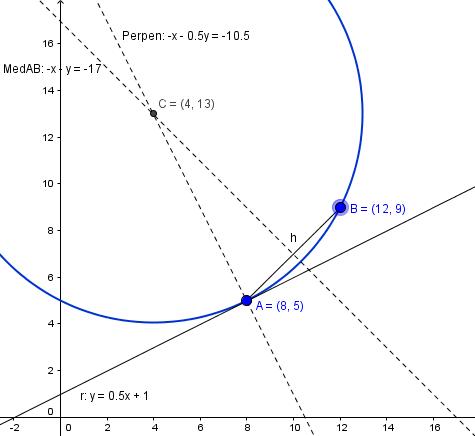
Primero calculamos la recta perpendicular que pasa por el punto de tangencia A(8,5)
La pendiente de la perpendicular es
m' = -1/m = -1 / (1/2) = -2
Y la ecuación es
y-5 = -2(x-8)
y = -2x +21
Ahora hay que encontrar un punto de esa recta que tenga la misma distancia a los puntos A y B. Si tiene la misma distancia también tendrá la misma distancia al cuadrado, luego nos evitamos poner las raices cuadradas.
$$\begin{align}&(x-8)^2 + (y-5)^2 = (x-12)^2+(y-9)^2\\&\\&x^2-16x+64 +y^2-10y+25=\\&x^2-24x+144+y^2-18y+81\\&\\&8x+8y=144+81-64-25 = 136\\&\\&\text{Y sustituimos y por su valor en la otra ecuación}\\&\\&8x+8(-2x+21) = 136\\&\\&8x -16x + 168 = 136\\&-8x =-32\\&x=4\\&y=-2·4+21 = 13\\&\\&\text{Luego el centro es }(4,13)\\&\text{Y el radio la distancia del centro al punto A o B}\\&\\&R= \sqrt{(4-8)^2+(13-5)^2}=\sqrt{16+64}=\sqrt {80}\\&\\&\text{Luego la ecuación de la circunferencia}\\&(x-h)^2+(y-k)^2= R ^2\\&es\\&(x-4)^2+(y-13)^2=80\end{align}$$:
:
