Resolver un límite indeterminado con cotangente

Perdona, copié mal el enunciado.

$$\begin{align}&\lim_{x\to 0}\left(\frac 1{x^2}-ctg^2\,x  \right)=\lim_{x\to 0}\left(\frac 1{x^2}-\frac{\cos^2 x}{sen^2x}  \right)=\\&\\&\lim_{x\to0}\frac{sen^2x-x^2cos^2x}{x^2sen^2x}= \frac 00=\\&\\&\text{No se puede hacer otra cosa que aplicar l'Hôpital}\\&\\&=\lim_{x\to 0} \frac{2senx\,cosx-2x\,\cos^2x+2x^2cos x\;senx}{2x\,sen^2x+2x^2sen x\,\cos x}=\frac{0}{0}=\\&\\&\text{sabemos que }\\&2senx\,cosx = sen \,2x\\&\text{eso ayudará bastante}\\&\\&=\lim_{x\to 0} \frac{sen\,2x-2x\,\cos^2x+x^2sen\,2x}{2x\,sen^2x+x^2sen\,2x}=\\&\\&=\lim_{x\to 0} \frac{(x^2+1)sen\,2x-2x\,\cos^2x}{2x\,sen^2x+x^2sen\,2x}=\\&\\&\text{derivamos otra vez}\\&\\&=\lim_{x\to 0} \frac{2x\,sen \,2x+2(x^2+1)\cos 2x-2cos^2x+4x\,\cos x\,sen x}{2sen^2x+4x\,senx\,\cos+2x\, sen\,2x+2x^2\,\cos 2x}= \\&\\&\frac{0+2-2+0}{0+0+0+0}= \frac 00=\\&\\&=\lim_{x\to 0} \frac{2x\,sen \,2x+2(x^2+1)\cos 2x-2cos^2x+2x\,sen\,2 x}{2sen^2x+2x\,sen\,2x+2x\, sen\,2x+2x^2\,\cos 2x}= \\&\\&\lim_{x\to 0} \frac{4x sen \,2x+2(x^2+1)\cos\,2x-2 \cos^2 x}{2sen^2x+4x\,sen\,2x+2x^2cos2x}=\\&\\&\text{derivamos de nuevo}\\&\\&=\lim_{x\to 0}\frac{4 sen\,2x+8x\,\cos 2x+4x\,\cos 2x-4(x^2+1)sen \,2x+4cosx\, senx}{}\end{align}$$

Y aquí la dejamos porque veo que el numerador seguirá siendo 0.

He hecho el ejercicio con un programa de ordenador, es en la cuarta derivada donde numerador y denominador dejan de valer 0 y el resultado es

lim = 16/24 = 2/3

que coincide con lo que dice la gráfica de la función

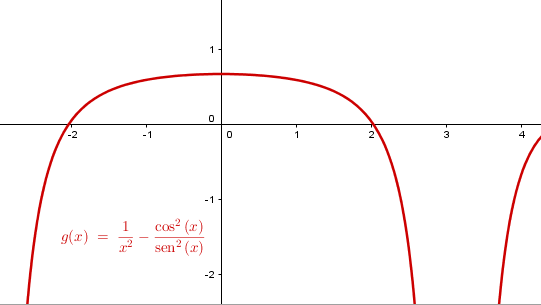
Y eso es todo, saludos.

:

: