¿Qué tipo de comportamiento describiría esta función?
Considerando que en el modelo de Malthus se tiene un parámetro que negativo, por ejemplo que = -0.5, responde las siguientes preguntas:
¿Qué tipo de comportamiento describiría esta función?
¿Qué pasa con la población conforme avanza el tiempo?
¿Qué condiciones se necesitan para que la población desaparezca?
Para profundizar en el principio de población de Malthus puedes estudiar el siguiente video:
1. En tu primera participación, comenta tus resultados y comparte el dibujo de la forma de tu gráfica (toma una foto).
1 respuesta
·
·
¡Hola Isa!
La primera pregunta es muy vaga, el comportamiento tiene muchos significados. La función es decreciente, responde al comportamiento de una población que decrece, por ejemplo una sustancia radiactiva o una población compuesta solo por personas en edad ya no fértil.
Es que no sabía que poner en la primera pregunta sin que fiera lo mismo que en la segunda. Conforme pasa el tiempo la población va decreciendo.
Para que la población desaparezca se necesita que el parámetro (el coeficiente del exponente) sea negativo.
La gráfica será la gráfica de una función:
$$\begin{align}&P(t) = P_0e^{-0.5t}\\&\\&\text{Tomaré por ejemplo }P_0=1000\\&\\&P(t)=1000e^{-0.5t}\end{align}$$Esta es la gráfica:
Y este es el enlace al fichero de la gráfica con Geogebra: Exponencial Malthus k=-0.5
Y eso es todo, sa lu dos.
:
:
¡Gracias! Profesor tengo una duda, lo que pasa es que esta semana veremos ecuaciones diferenciales, y nos pide en esta tarea pasar de derivada a diferencial entonces no se si así como la puso usted lo es.
Yo no resolví la ecuación diferencial porque ya la resolvían en el vídeo, entonces pensé que no haría falta sino poner directamente la solución del vídeo. Si se necesita hacer más trabajo será lo que sale en el vídeo.
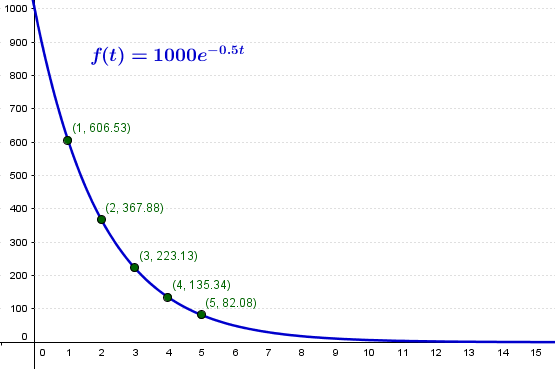
¿De dónde salen los 1000 con los que hace la gráfica? - cris zamora
El enunciado no decía ninguna población inicial y para hacer la gráfica se necesita que la función tenga una población inicial, puse esa como podría haber puesto cualquier otra. - Valero Angel Serrano Mercadal