Resolver el movimiento armónico simple
- Reúne los requerimientos para realizar el experimento que describe el movimiento armónico simple.
Requerimientos:
– Un hilo de 20 cm que pueda soportar el peso del siguiente objeto.
– Un objeto con un peso aproximado de 30 gramos y un área de 2 cm2 (puede ser una tuerca, tornillo, etc.).
– Un cronómetro (puede ser de la aplicación de un celular).
– Localiza en tu casa un espacio para que el objeto cuelgue y quede suspendido en el aire para que pueda oscilar libremente, sin que obstaculice el movimiento (puede ser el marco de una puerta, una ventana, un barandal, etc.).
- Lee con atención el procedimiento, las veces que creas necesarias, y procede a realizarlo.
Procedimiento para el cálculo de periodo de forma experimental:
- Amarra un extremo del hilo de 20 cm al objeto de 30 gramos, y el otro extremo fíjalo al espacio, estructura o artefacto que localizaste previamente, con el propósito de que quede colgando.
- Separa el péndulo de la posición vertical un ángulo pequeño (menor de 10º) y dejarlo oscilar libremente.
- Verifica que la oscilación se produzca en un plano vertical.
- Cuando estés seguro de que las oscilaciones son regulares (después de 2 ó 3 oscilaciones), pon en marcha el cronómetro y cuenta el número de oscilaciones completas a partir de la máxima separación del equilibrio.
Nota: se aconseja tomar N = 10, en el entendido de que una oscilación completa dura el tiempo de ida y vuelta hasta la posición donde se tomó el origen de tiempos.
- El periodo del péndulo es igual al tiempo medido dividido por N.
- Se repite la medida anterior un total de cinco veces con el mismo péndulo. Para poder sacar un promedio entre ellas y obtener un resultado más exacto.
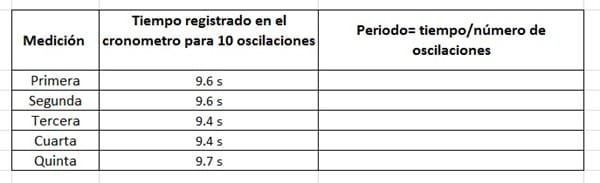
- Registra las mediciones en la siguiente tabla:
Esta es la tabla ya con los datos que obtuve con el experimento que realize
- Resuelve lo siguiente:
– Saca el promedio (es la suma los periodos calculados en cada registro dividido entre el número de mediciones).
– Obtén el periodo.
– Responde con tus propias palabras: ¿Qué es lo que representa el resultado anterior?
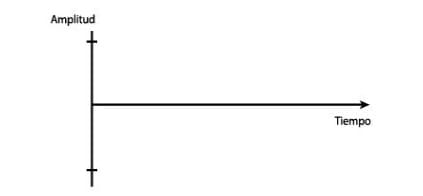
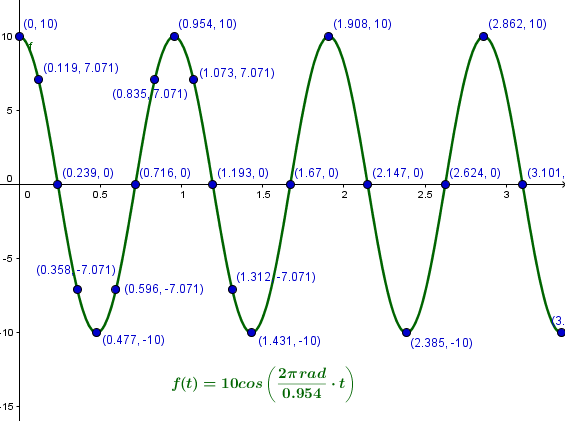
– A manera de hipótesis, imagina que se tuviera una amplitud de 10 cm, representa los resultados anteriores en la siguiente gráfica.
- Integra el reporte (de preferencia en procesador de textos) con los siguientes elementos:
- Describe el experimento que realizaste, incorpora la tabla de registros.
- Expón tus resultados junto con la gráfica.
- Expresa una breve conclusión clara y pertinente, respecto al uso del péndulo en el movimiento armónico simple.
1 Respuesta
·
·
¡Hola Angie!
Por fin alguien que manda todos los gráficos y tablas del problema este.
Yo hasta ahora tenía contestado esto:
No obstante voy a intentar hacerlo sin ver las imágenes. No voy a hacer el péndulo, pero por la teoría se sabe que el periodo es
$$\begin{align}&T = 2\pi·\sqrt {\frac lg} = 2Pi \sqrt{\frac{0.2m}{9.81m/s^2}}=\\&\\& 2\pi \sqrt{0.02038735984s^2}=0.89714\,s\end{align}$$Luego ya sabemos lo que dura un ciclo, como son 10 digamos que el tiempo ha sido 9 segundos por ejemplo, o di 9.1 o 8.9 o lo que quieras no muy alejado de ese tiempo.
·
Veo que los tiempos que has dado son un poco mayores pero no desentonan mucho delo que dice la teoría
El calculo del periodo es muy sencillo, es el tiempo total entre el número de oscilaciones. Como son diez oscilaciones divides entre 10 y el la tercera columna debes poner
0.96s
0.96s
0.94s
0.94s
0.97s
Y para obtener el periodo hacemos el promedio de estos, los sumamos y dividimos entre 5
T = (0.96+0.96+0.94+0.94+0.97) / 5 = 0.954s
“Péndulo”, “Periodo”, “Frecuencia”, “Amplitud” y “Funciones, seno y coseno, Experimenta con el “Movimiento armónico simple" - Física - Todoexpertos.com
El resultado anterior indica el tiempo que le cuesta al tornillo del péndulo ir desde un extremo al otro y volver.
·
Para hacer la gráfica, tienes que poner el el eje x el tiempo. Entonces en t=0 el péndulo está en su mayor amplitud, luego marcas el 10, en t = 0.954 vuelve a estar en ese mismo punto, marcas el 10. Y lo mismo en t = 0.954·2 = 1.908s, en t=0.954·3 = 2.862, etc.
Luego en los tiempos intermedios entre periodos el péndulo está en el otro lado luego marcas -10 para t = 0.954/2 = 0.477s, para t=0.477+0.954=1.431s, para t=0.477+2·0.954 = 2.385s
Y en los tiempos intermedios entre los que tenemos la función vale 0, luego en los puntos 0.954/4 , 0.954·(3/4), 0.954·(5/4), 0.954·(7/4) vale 0
Y si necesitas más puntos en los intermedios de estos tendremos ángulos de 45º cuyo coseno es raíz(2)/2 = 0.7071067812
Así en los puntos 0.954/8, 0.954·(7/8), 0.954·(9/8), 0.954·(15/8) valdrá 7.071067812
Y en los puntos 0.954·(3/8), 0.954(5/8), 0.954·(11/8), 0.954·(13/8) valdrá -7.071067812
Y en resumen, la gráfica es la de una función:
f(t) = 10*cos(wt)
la velocidad angular se calcula como:
w= 2pi rad / T = 2pi rad / 0.954 = 6.586148121 rad/s
Luego la gráfica es la de:
f(t) = 10cos(6,586148121·t)
De ahí es de donde puedes sacar todos los valores que quieras de la función
Ahora voy a comprobarlo.
EL fichero Geogebrá está aquí: Fichero Geogebra gráfica péndulo
Y eso es todo, espero que te sirva.
Saludos.
:
:
Este es un fichero de Geogebra mejor, pero es tan personal que si lo usáis sin cambiar cosas se darán cuenta que lo habéis sacado del mismo sitio. Os puede servir para generar la tabla.
Poniendo en la celda B1 el periodo que hayáis obtenido, se genera toda la gráfica: Gráfica Geogebra péndulo de tornillo 2.0
Y eso es todo, saludos.
:
:
Es mucho mejor la gráfica en Geogebra pero `para los que la habéis pedido en Excel aquí está la hoja de cálculo: Gráfica Excel Péndulo
Así es como queda, la podéis mejorar mucho si queréis.
Y eso es todo, saludos.
_
_
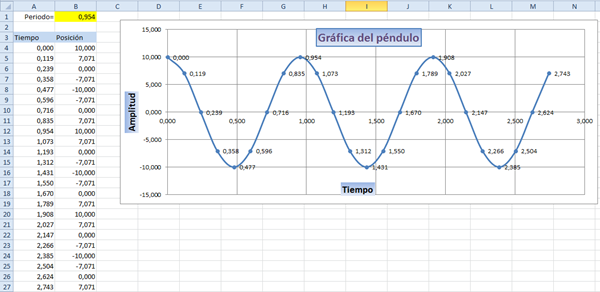
Profesor, quiero hacer la gráfica con excel y no me sale, me ayuda por favor. Gracias - Anónimo
Si hola buenas tardes también intente hacerlo por excel pero no quedo bien. - mario Dominguez
Ahora mismo en ordenador donde tengo Excel está entregado a una labor en Linux que no se puede parar y le puede llevar algún día de trabajo. Luego probaré en otro con un Excel de tiempo limitado a ver si me deja hacerlo, pero no va a ser inmediatamente. Tu tienes que usar la función que te pone en la gráfica y es probable que haya que tomar más intervalos de tiempo para que la curva quede bien, pero eso no lo he probado todavía. - Valero Angel Serrano Mercadal
Ya añadí una hoja de Cálculo parea hacer la gráfica con Excel. Se pone en la casilla amarilla el periodo y espero que salga todo con eso. - Valero Angel Serrano Mercadal
Gracias por su apoyo - pablo ortega
Esta perfecto y claro... Solo cabria, a mi criterio, hacer la observación siguiente. Como dan el valor de la masa oscilante = 30 gramos ( y la superficie expuesta= 2 cm^2)... seria un péndulo físico (no ideal)... en la fórmula debería considerarse el Momento de Inercia respecto de la suspensión. Igualmente el periodo estaría dando muy cercano al del péndulo ideal de masa despreciable... seria interesante que el alumno le haga notar esto al su docente... Tampoco se para que indican la superficie expuesta... - albert buscapolos Ing°
ALbertx, tienes razón. Pero estos ejercicios son de un plan de enseñanza secundaria en linea. Para ese nivel no creo que les exijan más que el modelo ideal del péndulo, los datos innecesarios los dan para que se hagan una idea de lo que tienen que construir. - Valero Angel Serrano Mercadal
Profesor gracias por su ayuda pero me dicen lo siguiente: Con respecto al contenido de la actividad realizas el experimento adoptando un péndulo, muestras evidencia de tu péndulo. Tomas los 5 tiempos de las oscilaciones completas pero considerando que son 10 oscilaciones completas, es decir desde el punto de donde se suelta hasta que se pandea al otro lado y regresa se me hace muy poco tiempo menos de 1 segundo para 10 oscilaciones, si pudieras comprobar tus tiempos. - Gaby Montes
Veo que te confundes un poco con las indicaciones ya que veo que calculas tiempos intermedios, velocidad angular y hasta obtienes la función de la gráfica los cuales no se solicitan en la actividad.Lo que tienes que hacer es obtener tu periodo promedio total, tú sacaste el promedio de los tiempos pero de lo que debes sacar promedio es de los periodos, los sumas y los divides entre - Gaby Montes
5. Debes responder con tus propias palabras¿Qué es lo que representa el resultado anterior?Después a manera de hipótesis y considerando una amplitud de 10 dibujar como seria la gráfica de la onda y por último te está faltando integrar tus conclusiones finales de todo el experimento. Te recomiendo que la gráfica la realicen a mano de forma más simple, únicamente con lo que se solicita. Debes responder con tus propias palabras¿Qué es lo que representa el resultado anterior? - Gaby Montes
Después a manera de hipótesis y considerando una amplitud de 10 dibujar como seria la gráfica de la onda y por último te está faltando integrar tus conclusiones finales de todo el experimento. Te recomiendo que la gráfica la realicen a mano de forma más simple, únicamente con lo que se solicita. - Gaby Montes
Gabi, con respecto al primer comentario. El ciclo es de menos de 1 segundo, ya te dije que teóricamente es 0.89 segundos luego las cifras que has puesto están muy bien y el que no sabe es el profesor. Respecto del segundo no entiendo lo que quiere decir el profesor, la gráfica es esa. ¿Si no piden eso en que consiste el problema? ¿En sumar 5 cifras y dividir por 50? Pues vaya chorrada de problema. Y el tercero esta relacionado con el segundo, no sé lo que quiere. ¿Este profesor sabe Física? - Valero Angel Serrano Mercadal
No, por eso acudo con usted y me puso una nota de 88 comparada a las de 100 anteriores, gracias profesor. Que hago en este caso? - Gaby Montes
maestro como siempre sus respuestas son las mejores es usted grande, yo hice esta misma pregunta pero con distintos numero podrá ayudarme el nuevo ejercicio quedaría así – Un listón de 25 cm que pueda soportar el peso del siguiente objeto.– Un objeto con un peso aproximado de 40 gramos y un área de 3 cm2 (puede ser una tuerca, tornillo, una goma de borrar, un frasco pequeño, etc.).a. Amarra un extremo del listón de 25 cm al objeto de 40 gramos, y el otro extremo fíjalo al espacio, estructura o artefacto que localizaste previamente, con el propósito de que quede colgando. - Cobali Arce
Cobali, es lo mismo, lo único que donde ponía 0,2 de longitud pones ahora 0.25 y el tiempo teórico sería de 1.0030 segundos, para redondear 1 segundo - Valero Angel Serrano Mercadal
muchas gracias maestro es un genio!! - Cobali Arce