Calcular la razón entre los volúmenes de una esfera y el cono

;)
Hola moises!

Como nuevo en el foro te recuerdo que lo único que se pide es que votes las respuestas.

En matemáticas vota Excelente a los expertos y te asegurarás nuevas respuestas.

Y más en un problemita como este

Si hacemos una sección frontal de la situación:

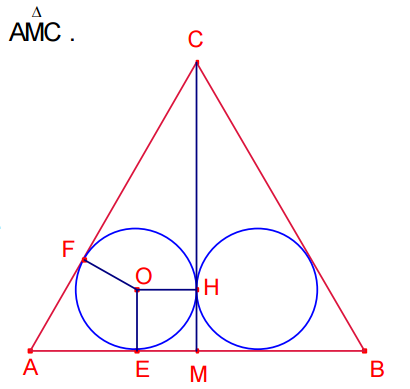
Sea    OH=OE=OF= r  (radio esfera)

Sea    MB=MA= R   (radio base cono)

CM= h   (altura cono)

CB=g=5r    (generatriz del cono)

$$\begin{align}&\frac{V_{esfera}}{V_{cono}}=\frac{ \frac{4}{3} \pi r^3}{\frac{1}{3} \pi R^2 h}=\frac{4r^3}{R^2 h}\end{align}$$

hemos de relacionar r, R  i   h.

Pitágoras en el triangulo MBC:

$$\begin{align}&g^2=h^2+R^2\\&(5r)^2=h^2+R^2\\&\\&25r^2=h^2+R^2 \ \ \ \ (1)\end{align}$$

por otro lado las tangentes desde un mismo punto exterior a una circunferencia miden lo mismo. Aprovechando este hecho, tenemos que:

tangentes desde C

CF=CH

CH=CM-MH=h-r

tangentes desde A:

AF=AE

AE=AM-EM=R-r

CF+AF=g

(h-r)+(R-r)=5r   ===>     h+r=7r              (2)

De (1):

$$\begin{align}&R=\sqrt{25r^2-h^2}\\&\\&Sustituyendo \ en \ (2):\\&\\&h=7r-R\\&h=7r-\sqrt{25r^2-h^2}\\&\\&\sqrt{25r^2-h^2}=7r-h\\&\\&elevando \ al \ cuadrado:\\&\\&25r^2-h^2=49r^2-14rh+h^2\\&\\&0=2h^2-14rh+24r^2\\&ecuación \ de \ segundo \ grado \ en \ h\\&\\&h^2-7rh+12r^2=0\\&\\&h=\frac{7r \pm \sqrt{49r^2-48r^2}}{2}=\frac{7r \pm r}{2}=\\&\\&h_1=4r\\&h_2=3r\\&\\&Si \ h=3r \Rightarrow R=7r-h=7r-3r=4r \Rightarrow h \ < R\\&\\&\\&\\&Si \ h=4r \Rightarrow R=7r-h=7r-4r=3r \Rightarrow h \ >R\\&\\&Luego:\\&h=4r\\&R=3r\\&\\&\frac{V_{esfera}}{V_{cono}}=\frac{4r^3}{R^2h}=\frac{4r^3}{9r^2·4r}=\frac{4}{36}=\frac{1}{9}\end{align}$$

Espero que te sirva

Saludos

Bonito problema

;)

;)

;)
Escribí mal (2):

h+R=7r

Pero todo es correcto

;)

;)