Si estudias el lugar geométrico de todas las parábolas de tiro ( ideales) que representan las distintas trayectorias de un proyectil determinado lanzado con velocidad inicial Vo y angulo variable entre 90 y 0°, encontrás que están contenidas dentro de una parábola envolvente llamada " de seguridad". Se llama así porque permite a los barcos - por ejemplo - ubicarse fuera de la trayectoria de proyectiles enemigos.
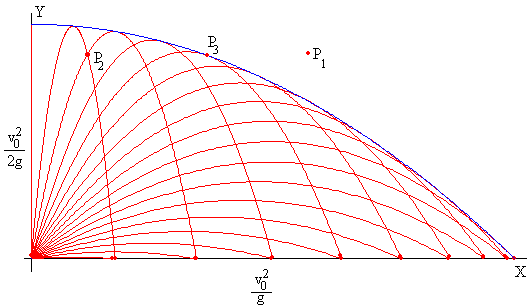
En veerticales..yMax.= altura maxima que alcanza el proyectil. En horizontal: los respectivos alcances. Velocidad de lanzamiento=Vo en todos los casos... lo que varia es el angulo.
Analizamos aquí que el punto p2 representa la altura de la montaña. Es la cota limite que el proyectil atacante deberá sortear para llegar al área enemiga.
Hay dos parábolas que alcanzan ese punto P2 ... el atacante elige la inclinación mayor para la cual el proyectil tendrá el alcance mínimo posible sorteando la montaña.
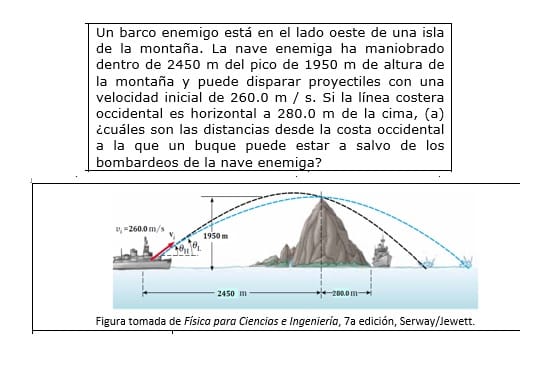
Luego serian: Coordenadas de P2 =......X= 2450 METROS .............Y=1950 METROS.-
La ecuacion de la trayectoria del proyectil como funcion de x e y parte de:
x= Vo cosfi. t ........................y = Vo sen fi t - 1/2 g t^2
Si despejas t entre ambas llegas a que y = x tg. Fi - g x^2/ (2Vo^2 cos^2 fi)
Que la podes modificar algebraicamente de manera de llegar a la siguiente ecuación de la trayectoria del proyectil:
tg^2 fi - 2 Vo^2/ g x tg fi + ( 1 + 2 Vo^2 y / g x^2) = 0.....................que es una cuadratica en tg fi.
La resolución te dará dos valores del angulo de lanzamiento fi. El tirador sabe que hay una inclinación a partir de la cual la montaña no dejara pasar el proyectil al otro lado.
Hallas los términos incógnitas:
2 Vo^2/ g x = 2 x 260^2 / 10 x 2450 = 5.518
( 1 + 2 Vo^2 y / g x^2) = 5.392
tg^fi - 5.518 tg fi + 5.392 = 0
Que resuelta da los valores del angulo de inclinación ( son dos) :tg fi1= 1.2682 y tg fi2=
4.252
Eligiendo la inclinación mayor... que seria (tg fi2)^-1 = 76.76° tienes la menor distancia de la costa que podrá llegar el proyectil el atacante.
Ahora para saber el alcance ´para ese tiro a 260 m/seg. y 76.76° de elevación aplicas:
Alcance = (Vo^2 / g) sen 2fi = (260^2/ 10) sen 153.53 = 3013 metros.
Como tienes 280 metros desde la cima de la montaña hasta la costa... serian 2450 + 280 = 2730 metros desde el cañón atacante hasta la costa opuesta... como el alcance del tiro era de 3013 metros... el barco debería ubicarse entre la costa y ( 3013 - 2730) = 283 m máximos mar adentro para estar a salvo del enemigo.
NOTA: Tome g= 10 m/seg^2 en todo el calculo.